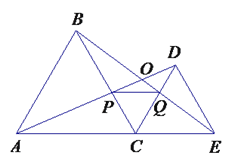
【题目】如右图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°. 恒成立的结论有( )
A. ①③④⑤ B. ①②④⑤
C. ①②③⑤ D. ①②③④
参考答案:
【答案】C
【解析】分析:本题是三角形全等的综合题,利用三角形全等逐个解决就可以.
解析:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,∴AC=BC,EC=DC,∠BCE=∠ACD=120°∴△ACD≌△ECB∴AD=BE,故本选项正确;②∵△ACD≌△ECB∴∠CBQ=∠CAP,又∵∠PCQ=∠ACB=60°,CB=AC,∴△BCQ≌△ACP,∴CQ=CP,又∠PCQ=60°,∴△PCQ为等边三角形,∴∠QPC=60°=∠ACB,∴PQ∥AE,故本选项正确;③∵∠ACB=∠DCE=60°,∴∠BCD=60°,∴∠ACP=∠BCQ,∵AC=BC,∠DAC=∠QBC,∴△ACP≌△BCQ(ASA),∴CP=CQ,AP=BQ,故本选项正确;④已知△ABC、△DCE为正三角形,故∠DCE=∠BCA=60°,∠DCB=60°,又因为∠DPC=∠DAC+∠BCA,∠BCA=60°,∠DPC>60°,故DP不等于DE,故本选项错误;⑤∵△ABC、△DCE为正三角形,∴∠ACB=∠DCE=60°,AC=BC,DC=EC,∴∠ACB+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴∠CAD=∠CBE,∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,∵∠ACB=∠CBE+∠CEB=60°,∴∠AOB=60°,故本选项正确.
综上所述,正确的结论是①②③⑤.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①(﹣2)101+(﹣2)100=﹣2100;②20172+2017一定可以被2018整除;③16.9×
 +15.1×
+15.1× 能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)27﹣16+(﹣7)﹣18;
(2)(﹣6)×(﹣
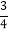 )÷(﹣
)÷(﹣ );
);(3)(
 ﹣
﹣ ﹣
﹣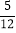 )×60;
)×60;(4)﹣24+3×(﹣1)4﹣(﹣2)3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况探索结论
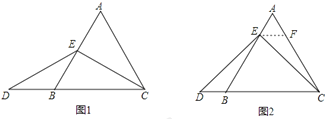
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE__________DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE__________DB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车行驶时油箱中余油量Q(L)与行驶时间t(h)的关系如表:
行驶时间t/h
余油量Q/L
1
42
2
34
3
26
4
18
5
10
(1)汽车行驶之前油箱中有汽油多少升?
(2)用行驶时间t的代数式表示余油量Q(直接写出答案);
(3)当t=
 时,求余油量Q的值.
时,求余油量Q的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:(1)13=
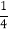 ×12×22;(2)13+23=
×12×22;(2)13+23=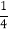 ×22×32;(3)13+23+33=
×22×32;(3)13+23+33=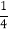 ×32×42;(4)13+23+33+43=
×32×42;(4)13+23+33+43=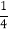 ×42×52;
×42×52;
根据上述等式的规律,解答下列问题:
(1)写出第5个等式:_____;
(2)写出第n个等式(用含有n的代数式表示);
(3)设s是正整数且s≥2,应用你发现的规律,化简:
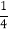 ×s2×(s+1)2﹣
×s2×(s+1)2﹣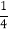 ×(s﹣1)2×s2.
×(s﹣1)2×s2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G.
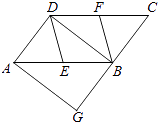
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
相关试题

