【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.

参考答案:
【答案】3
【解析】
试题分析:利用矩形的面积公式得到ABBC=32,再根据旋转的性质得AB=DE,OD=OA,接着利用正切的定义得到an∠DOE=![]() ,所以DE2DE=32,解得DE=4,于是得到AB=4,OA=8,同样在Rt△OCM中利用正切定义得到tan∠COM=
,所以DE2DE=32,解得DE=4,于是得到AB=4,OA=8,同样在Rt△OCM中利用正切定义得到tan∠COM=![]() ,由OC=AB=4,可求得MC=2,则M(﹣2,4),易得反比例函数解析式为y=﹣
,由OC=AB=4,可求得MC=2,则M(﹣2,4),易得反比例函数解析式为y=﹣![]() ,然后确定N点坐标(﹣8,1),可知BN=4﹣1=3.
,然后确定N点坐标(﹣8,1),可知BN=4﹣1=3.
故答案为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的长为5×102cm,宽为3×102cm,则它的面积是cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(-4,3)、B(-2,-3)
(1)描出A、B两点的位置,并连结AB、AO、BO。
(2)△AOB的面积是__________。
把△AOB向右平移4个单位,再向上平移2个单位,画出平移后的△A′B′C′,并写出各点的坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:如果关于
的一元二次方程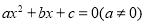 有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:
有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:①方程
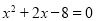 是倍根方程;
是倍根方程;②若关于
的方程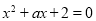 是倍根方程,则a=±3;
是倍根方程,则a=±3;③若关于x的方程
 是倍根方程,则抛物线
是倍根方程,则抛物线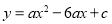 与x轴的公共点的坐标是(2,0)和(4,0);
与x轴的公共点的坐标是(2,0)和(4,0);④若点(m,n)在反比例函数
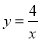 的图象上,则关于x的方程
的图象上,则关于x的方程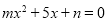 是倍根方程
是倍根方程上述结论中正确的有( )
A.①② B.③④ C.②③ D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数是( )
①一个有理数不是整数就是分数;②一个有理数不是正数就是负数;③一个整数不是正的就是负的;④一个分数不是正的,就是负的.
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣2x=0的根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方
 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ .计算结果保留根号)
.计算结果保留根号)
相关试题

