【题目】已知反比例函数y=![]() 的图象与一次函数y=k2x+m的图象交于A(a,1)、B(
的图象与一次函数y=k2x+m的图象交于A(a,1)、B(![]() ,﹣3)两点,连结AO.
,﹣3)两点,连结AO.
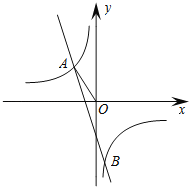
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出k2x+m﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)设点C在y轴上,且与点A、O构成等腰三角形,请直接写出点C的坐标.
参考答案:
【答案】(1)反比例函数关系式为y=﹣![]() ,一次函数关系式为y=﹣3x﹣2;(2)﹣1<x<0或x>
,一次函数关系式为y=﹣3x﹣2;(2)﹣1<x<0或x>![]() ;(3)点C的坐标为:(0,﹣
;(3)点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() )或(0,2)或(0,1).
)或(0,2)或(0,1).
【解析】
试题分析:(1)将点A(﹣1,a)、B(![]() ,﹣3)代入反比例函数y=
,﹣3)代入反比例函数y=![]() 中得:﹣3×
中得:﹣3×![]() =(﹣1)×a=k1,可求k1、a;再将点A(﹣1,a)、B(
=(﹣1)×a=k1,可求k1、a;再将点A(﹣1,a)、B(![]() ,﹣3)代入y2=k2x+m中,列方程组求k2、m即可;
,﹣3)代入y2=k2x+m中,列方程组求k2、m即可;
(2)根据图象得到一次函数在反比例函数下方时x的取值范围即可求解;
(3)分三种情况:①OA=OC;②AO=AC;③CA=CO;讨论可得点C的坐标.
解:(1)∵反比例函数y=![]() 的图象经过B(
的图象经过B(![]() ,﹣3),
,﹣3),
∴k1=3×![]() ×(﹣3)=﹣3,
×(﹣3)=﹣3,
∵反比例函数y=![]() 的图象经过点A(﹣1,a),
的图象经过点A(﹣1,a),
∴a=1.
由直线y2=k2x+m过点A,B得: ,
,
解得![]() .
.
∴反比例函数关系式为y=﹣![]() ,一次函数关系式为y=﹣3x﹣2;
,一次函数关系式为y=﹣3x﹣2;
(2)k2x+m﹣![]() <0的x的取值范围为﹣1<x<0或x>
<0的x的取值范围为﹣1<x<0或x>![]() ;
;
(3)OA=![]() =
=![]() ,
,
如图,线段OA的垂直平分线与y轴的交点,有1个,点C的坐标为:(0,1);
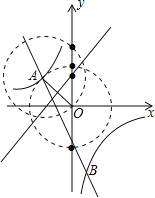
以点A为圆心、AO长为半径的圆与y轴的交点,有1个,点C的坐标为:(0,2);
以点O为圆心、OA长为半径的圆与y轴的交点,有2个,点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() ).
).
故点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() )或(0,2)或(0,1).
)或(0,2)或(0,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据:7,a,8,b,10,c,6的平均数是4.
(1)求a,b,c的平均数;
(2)求2a+1,2b+1,2c+1的平均数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要估计鱼塘中的鱼数,养鱼者首先从鱼塘中打捞了50条鱼,在每条鱼身上做好记号后把这些鱼放归鱼塘,再从鱼塘中打捞100条,发现只有两条鱼是刚才做了记号的鱼,假设在鱼塘内鱼均匀分布,那么估计这个鱼塘的鱼数约为( )
A. 5000条 B. 2500条 C. 1750条 D. 1250条
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2+7x+12=0。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中(∠C=90°),放置边长分别为3,4,x的三个正方形,则x的值为( )
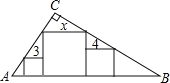
A.5 B.6 C.7 D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )
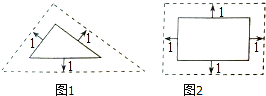
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面等式成立的是( )
A.83.5°=83°50′
B.37°12′36″=37.48°
C.24°24′24″=24.44°
D.41.25°=41°15′
相关试题

