Question

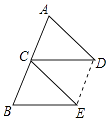
【题目】如图，点C是AB的中点，AD=CE，CD=BE．
（1）求证：△ACD≌△CBE；
（2）连接DE，求证：四边形CBED是平行四边形．

Answer 1

【答案】
（1）证明：∵点C是AB的中点，

∴AC=BC；在△ADC与△CEB中， ，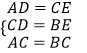

∴△ADC≌△CEB（SSS）

（2）证明：连接DE，如图所示：

∵△ADC≌△CEB，

∴∠ACD=∠CBE，

∴CD∥BE，

又∵CD=BE，

∴四边形CBED是平行四边形．

【解析】（1）由SSS证明证明△ADC≌△CEB即可；（2）由全等三角形的性质得出得到∠ACD=∠CBE，证出CD∥BE，即可得出结论．
【考点精析】根据题目的已知条件，利用平行四边形的判定的相关知识可以得到问题的答案，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．