【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. 请解决下列问题: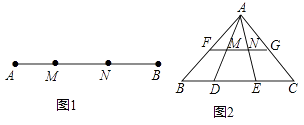
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.
参考答案:
【答案】
(1)解∵点M,N是线段AB的勾股分割点,且BN>MN>AM,AM=2,MN=3,
∴BN2=MN2+AM2=9+4=13,
∴BN= ![]()
(2)证明∵点F、M、N、G分别是AB、AD、AE、AC边上的中点,
∴FM、MN、NG分别是△ABD、△ADE、△AEC的中位线,
∴BD=2FM,DE=2MN,EC=2NG,
∵点D,E是线段BC的勾股分割点,且EC>DE>BD,
∴EC2=DE2+DB2,
∴4NG2=4MN2+4FM2,
∴NG2=MN2+FM2,
∴点M,N是线段FG的勾股分割点
【解析】(1)由M、N为线段AB的勾股分割点,利用题中的新定义列出关系式,将MN与AM的长代入求出BN的长即可;(2)由F、M、N、G分别为各边中点,得到FM、MN、NG分别为中位线,利用中位线定理得到BD=2FM,DE=2MN,EC=2NG,再利用题中新定义列出关系式,即可得证.
【考点精析】关于本题考查的勾股定理的概念和三角形中位线定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能得出正确答案.
-
科目: 来源: 题型:
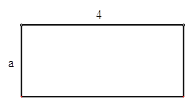
查看答案和解析>>【题目】如图,矩形的长为4,宽为a(a<4),剪去一个边长最大的正方形后剩下一个矩形,同样的方法操作,在剩下的矩形中再剪去一个最大的正方形,若剪去三个正方形后,剩下的恰好是一个正方形,则最后一个正方形的边长是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位计划购买电脑若干台,经了解同一型号市场预售价均为每台5000元.现有两商场优惠促销,甲商场:购买不超过2台按原价销售,超过2台的部分每台打7折;乙商场:每台均打8折.
(1)若学校购买5台,哪家商场较优惠?购买7台呢?
(2)买多少台时两商场所需费用一样多?
(3)你知道学校怎样选购更省钱?
【答案】(1)购买5台,乙商场更优惠;购买7台,甲商场更优惠;(2)6;(3)答案见解析.
【解析】试题分析:(1)根据甲乙两个商场的促销方案分别计算出学校购买5台和7台电脑所需的费用,比较即可;(2)设购买
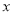 台时,两商场所需要费用一样多,根据费用一样多列出方程,解方程即可;(3)在(2)的基础上,比较即可.
台时,两商场所需要费用一样多,根据费用一样多列出方程,解方程即可;(3)在(2)的基础上,比较即可.试题解析:
(1)购买5台,甲商场:
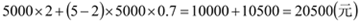
乙商场:
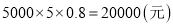 ,
,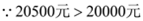 ,
,  乙商场更优惠.
乙商场更优惠.购买7台,甲商场:
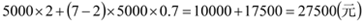 ,乙商场:
,乙商场: 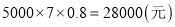 .
.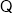 27500元<28000元,
27500元<28000元,  甲商场更优惠.
甲商场更优惠.(2)设购买
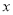 台时,两商场所需要费用一样多,根据题意得
台时,两商场所需要费用一样多,根据题意得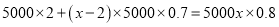 ,解得:
,解得: 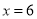 .
.答:当购买
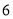 台时,两商场所需要费用一样多.
台时,两商场所需要费用一样多.(3)当购买台数小于6时,在乙商场更省钱;
当购买台数等于6时,两商场一样省钱;
当购买台数大于6时,在甲商场更省钱.
【题型】解答题
【结束】
26【题目】已知∠AOB=90°,
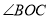 是锐角,ON平分
是锐角,ON平分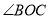 ,OM平分∠AOB.
,OM平分∠AOB.(1)如图1若
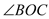 =30°,求
=30°,求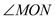 的度数?
的度数?(2)若射线OC绕着点O运动到∠AOB的内部(如图2),在(1)的条件下求
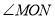 的度数;
的度数;(3)若∠AOB=
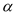 (90°≤
(90°≤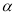 <180°),
<180°),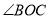 =
= 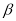 (0°<
(0°<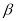 <90°),请用含有
<90°),请用含有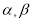 的式子直接表示上述两种情况
的式子直接表示上述两种情况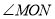 的度数.
的度数.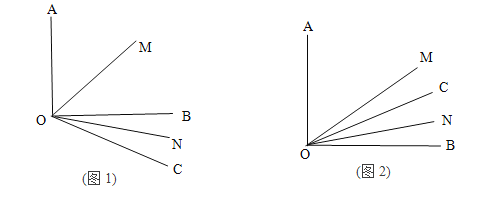
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是720°,这个多边形的边数是( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】若AD=8,AB=4,那么当BC=(____),CD=(____)时,四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在D′处,则重叠部分△AFC的面积是( )

A.8
B.10
C.20
D.32 -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据:5、-2、0、1、4的中位数是( )
A. 0 B. -2 C. 1 D. 4
相关试题

