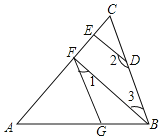
【题目】如图，于点E，于点F，，求证：．

试将下面的证明过程补充完整填空：

证明：，已知

______

同位角相等，两直线平行，

两直线平行，同旁内角互补，

又已知，

______，同角的补角相等

______内错角相等，两直线平行，

______

参考答案：

【答案】垂直的定义；；BC；两直线平行，同位角相等

【解析】

根据垂线的定义结合平行线的判定定理可得出，由平行线的性质可得出，结合可得出，从而得出。根据平行线的性质即可得出，此题得解.

证明： ，

（垂直的定义），

（同位角相等，两直线平行），

（两直线平行，同旁内角互补），

又 ，

（同角的补角相等），

（内错角相等，两直线平行），

（两直线平行，同位角相等）.

故答案为：垂直的定义；；；两直线平行，同位角相等.

关闭