【题目】一个正方形在平面直角坐标系内的位置如图所示,已知点 A 的坐标为(3,0),线段 AC与 BD 的交点是 M.
(1)写出点 M、B、C、D 的坐标;
(2)当正方形中的点 M 由现在的位置经过平移后,得到点 M(﹣4,6)时,写出点 A、B、
C、D 的对应点 A′、B′、C′、D′的坐标,并求出四边形 A′B′C′D′的面积

参考答案:
【答案】(1)点 M(3,3),点 B(6,3),点 C(3,6),点 D(0,3);(2)18.
【解析】分析:(1)根据正方形的性质结合直角坐标系可得出点M、B、C、D 的坐标.
(2)通过横坐标:右移加,左移减;纵坐标:上移加,下移减可得点 A′、B′、C′、D′,平移后的四边形A′B′C′D′的面积等于原来正方形ABCD的面积,所以算出正方形ABCD的面积即可.
详解:(1)根据正方形的性质结合直角坐标系可得:
点 M(3,3),点 B(6,3),点 C(3,6),点 D(0,3).
(2)点 M(3,3),平移后的坐标为(﹣4,6), 故可得平移是按照:向左平移 7 个单位,向上平移 3 个单位进行的, 故 A′(﹣4,3)、B′(﹣1,6)、C′(﹣4,9)、D′(﹣7,6).
AC 6, DM 3.
SACD ![]() ACDM
ACDM ![]() 6 3 9.
6 3 9.
S四边形ABCD S四边形ABCD 2SACD 18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定:正方形内部 不包含边界上的点.观察如图所示的中心在原点、一边平行于 x 轴的正方形:边长为 1 的正方形内部有 1 个整点,边长为 2 的正方形内部有 1 个整点,边长为 3 的正方形内部 有 9 个整点,…,则边长为 10 的正方形内的整点个数为( )

A. 64 个 B. 100 个 C. 81 个 D. 121 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.1cm,2cm,2cmB.1cm,2cm,4cm
C.2cm,3cm,5cmD.5cm,6cm,12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】五子棋深受广大棋友的喜爱,其规则是:在 15 15 的正方形棋盘中,由黑方先行,轮流奕子,在任何一方向(横向、竖向或斜线 方向)上连成五子者为胜。如图 3 是两个五子棋爱好者甲和乙的 部分对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若 A 点的位置记作(8,4),若不让乙在短时间内获胜,则甲必须落子 的位置是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的两个根,则实数x1 , x2 , a,b的大小关系为( )
A.x1<x2<a<b
B.x1<a<x2<b
C.x1<a<b<x2
D.a<x1<b<x2 -
科目: 来源: 题型:
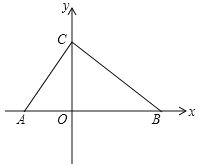
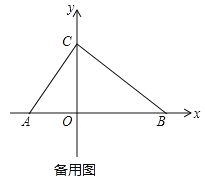
查看答案和解析>>【题目】如图,在平面直角坐标系内,点 O 为坐标原点,点 A 在 x 轴负半轴上,点 B、C 分别在 x 轴、y 轴正半轴上,且 OB=2OA,OB﹣OC=OC﹣OA=2.
(1)求点 C 的坐标;
(2)点 P 从点 A 出发以每秒 1 个单位的速度沿 AB 向点 B 匀速运动,同时点 Q 从点 B 出发 以每秒 3 个单位的速度沿 BA 向终点 A 匀速运动,当点 Q 到达终点 A 时,点 P、Q 均停止运 动,设点 P 运动的时间为 t 秒(t>0),线段 PQ 的长度为 y,用含 t 的式子表示 y,并写出 相应的 t 的范围;
(3)在(2)的条件下,过点 P 作 x 轴的垂线 PM,PM=PQ,是否存在 t 值使点 O 为 PQ 中 点?若存在求 t 值并求出此时三角形 CMQ 的面积;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)化简: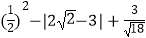 ;
;
(2)解方程: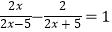 .
.
相关试题

