Question

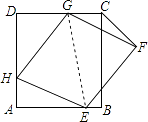
【题目】如图，菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上，连接CF．
（1）求证：∠HEA=∠CGF；
（2）当AH=DG时，求证：菱形EFGH为正方形．

Answer 1

【答案】
（1）证明：连接GE，

∵AB∥CD，

∴∠AEG=∠CGE，

∵GF∥HE，

∴∠HEG=∠FGE，

∴∠HEA=∠CGF

（2）证明：∵四边形ABCD是正方形，

∴∠D=∠A=90°，

∵四边形EFGH是菱形，

∴HG=HE，

在Rt△HAE和Rt△GDH中，

，

∴Rt△HAE≌Rt△GDH（HL），

∴∠AHE=∠DGH，又∠DHG+∠DGH=90°，

∴∠DHG+∠AHE=90°，

∴∠GHE=90°，

∴菱形EFGH为正方形；

【解析】（1）连接GE，根据正方形的性质和平行线的性质得到∠AEG=∠CGE，根据菱形的性质和平行线的性质得到∠HEG=∠FGE，解答即可；（2）证明Rt△HAE≌Rt△GDH，得到∠AHE=∠DGH，证明∠GHE=90°，根据正方形的判定定理证明．