【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,已知DE﹦DF,∠EDF=∠A。
(1)找出图中相似的三角形,并证明;
(2)求证: ![]() .
.

参考答案:
【答案】(1)△ABC∽△DEF,证明见解析;(2)证明见解析.
【解析】试题分析:此题的证明方法比较多,可以选择如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似,因为都是等腰三角形,对应边成比例,且夹角相等,所以相似;再利用相似三角形的对应边成比例证得: ![]() .
.
试题解析:(1)△DEF∽△ABC,△BDE∽△CEF.
证明如下:∵AB=AC,DE=DF,
∴![]() .
.
∵∠EDF=∠A,
∴△DEF∽△ABC.
∴∠DEF=∠B=∠C.
∵∠BED+∠DEF+∠FEC=∠C+∠CFE+∠FEC=180°,
∴∠BED=∠CFE.
∴△BDE∽△CEF.
(2)证明:∵△BDE∽△CEF,
∴![]() .
.
∵△DEF∽△ABC,
∴![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:
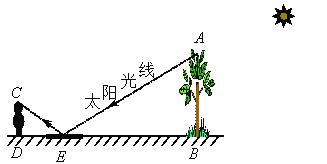
实践:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这是恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度(精确到0.1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?

-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
已知张强家.体育场.文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.据图象回答下列问题:
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
(2)张强在文具店停留了多少时间?
(3)张强从文具店回家平均每分钟走多少千米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为推进课改,王老师把班级里60名学生分成若干小组,每小组只能是5人或6人,则有几种分组方案( )
A. 4B. 3C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过________小时车库恰好停满.
相关试题

