【题目】如图①,先把一矩形![]() 纸片上下对折,设折痕为
纸片上下对折,设折痕为![]() ;如图②,再把
;如图②,再把
点![]() 叠在折痕线
叠在折痕线![]() 上,得到
上,得到![]()
![]() .过
.过![]() 点作
点作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)求证: ![]() ∽
∽![]() ;
;
(2)在图②中,如果沿直线![]() 再次折叠纸片,点
再次折叠纸片,点![]() 能否叠在直线
能否叠在直线![]() 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长度.
的长度.

参考答案:
【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)由题意可以得到∠BPE=∠AQB=90°,通过角的转化可以得到∠BEP=∠ABQ,从而可以得到△PBE∽△QAB;
(2)根据折叠的知识可以得到QB=PB,由第(1)问中的相似可以得到对应边成比例,通过转化可以得到△PBE∽△BAE,从而可以解答本题;
(3)由题意和第(2)问可以得到∠AEB=∠BEP=60°,∠ABE=90°,又因为AB=![]() ,sin∠AEB=
,sin∠AEB=![]() ,从而可以得到AE的长度.
,从而可以得到AE的长度.
试题解析:(1)证明:∵PQ⊥MN,BN∥EC∥AD,∴∠BPE=∠AQB=∠PBN=∠NBQ=90°,∴∠PBE+∠BEP=90°,又∵∠PBE+∠ABQ=180°﹣∠ABE=180°﹣90°=90°,∴∠BEP=∠ABQ,在△PBE和△QAB中,∵∠BPE=∠AQB,∠BEP=∠ABQ,∴△PBE∽△QAB;
(2)点A能叠在直线EC上,理由:∵△PBE∽△QAB,∴ ![]() ,∵由折叠可知,QB=PB,∴
,∵由折叠可知,QB=PB,∴![]() ,即
,即![]() ,又∵∠ABE=∠BPE=90°,∴△PBE∽△BAE,∴∠AEB=∠PEB,∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
,又∵∠ABE=∠BPE=90°,∴△PBE∽△BAE,∴∠AEB=∠PEB,∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
(3)解:由(2)可知,∠AEB=∠PEB,而由折叠过程知:2∠AEB+∠PEB=180°,∴∠AEB=∠PEB=60°,在Rt△ABE中,sin∠AEB=![]() ,∴AE=
,∴AE= .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2012年4月,受“毒胶囊”事件的影响,某种药品的价格大幅度下调,下调后每盒价格是原价的
 ,已知下调后每盒价格是10元/盒.
,已知下调后每盒价格是10元/盒. (1)该药品的原价是_______元;
(2)4月底,各部门加大了对胶囊生产的监管力度,因此,药品价格开始回升,经过两个月后,该药品价格上调为14.4元/盒. 问5、6月份该药品价格的月平均增长率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

-
科目: 来源: 题型:
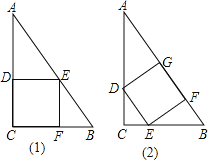
查看答案和解析>>【题目】直角三角形的铁片ABC的两条直角边BC,AC的长分别为3cm和4cm,如图所示分别采用⑴,⑵两种方法,剪去一块正方形铁片,为了使剪去正方形铁片后剩下的边角料较少,试比较哪一种剪法较为合理,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“你今天光盘了吗?”这是国家倡导厉行节约,反对浪费以来的时尚流行语,某校团委随机抽取部分了学生,对他们是否了解关于“光盘行动”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如下,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:

(1)求本次活动共调查了多少名学生?
(2)请补全图2,并求出图1中,B区域的圆心角度数;
(3)若该校有2400名学生,请估算该校不是了解很多的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现计划把1240吨甲种货物和880吨乙种货物用一列火车运往某地,已知这列火车挂有A、B两种不同规格的货车车厢共40节,使用A型车厢每节费用为6000元,B型车厢每节费用8000元.如果每节A型车厢最多可装35吨甲种货物和15吨乙种货物,每节B型车厢最多可装25吨甲种货物和35吨乙种货物;
(1)那么共有哪几种安排车厢的方案?
(2)在上述方案中,哪种方案运费最省、最少运费为多少元?
(3)在(1)问下,若两种货物全部售出,且每吨货物售出获利200元,除去运费获
利154000元,问:在这种情况下是按哪种方案安排车厢的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若式子
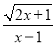 有意义,则
有意义,则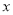 的取值范围是
的取值范围是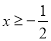 ;②正多边形的的一个内角是140°,则这个多边形是正九边形;③甲、乙两人进行射击测试,每人次射击成绩的平均数都是8.8环,方差分别是
;②正多边形的的一个内角是140°,则这个多边形是正九边形;③甲、乙两人进行射击测试,每人次射击成绩的平均数都是8.8环,方差分别是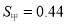 ,
,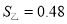 ,则射击成绩最稳定的是乙;④若
,则射击成绩最稳定的是乙;④若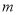 是方程
是方程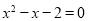 的一个实数根,则
的一个实数根,则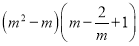 的值是4.其中正确的有( )个
的值是4.其中正确的有( )个A.1B.2C.3D.4
相关试题

