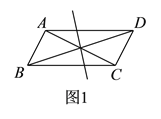
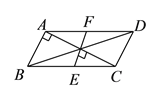
【题目】如图![]() ,平行四边形
,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .将直线
.将直线![]() 绕点
绕点![]() 顺时针旋转分别交
顺时针旋转分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(![]() )在旋转过程中,线段
)在旋转过程中,线段![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(![]() )如图
)如图![]() ,若
,若![]() ,当旋转角至少为__________
,当旋转角至少为__________![]() 时,四边形
时,四边形![]() 是平行四边形,并证明此时的四边形是
是平行四边形,并证明此时的四边形是![]() 是平行四边形.
是平行四边形.
参考答案:
【答案】(![]() )相等;(
)相等;(![]() )
)![]()
【解析】试题分析:(1)根据平行四边形的对边平行可得AD∥BC,对角线互相平分可得OA=OC,再根据两直线平行,内错角相等求出∠1=∠2,然后利用“角边角”证明△AOF和△COE全等,根据全等三角形对应边相等即可得到AF=CE
(2)根据垂直的定义可得∠BAO=90°,然后求出∠BAO=∠AOF,再根据内错角相等,两直线平行可得AB∥EF,然后根据平行四边形的对边平行求出AF∥BE,再根据两组对边分别平行的四边形是平行四边形证明;
试题解析:
(![]() )相等,理由如下:
)相等,理由如下:
如图所示:
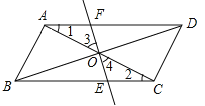
在ABCD中,AD∥BC,OA=OC,
∴∠1=∠2,
在△AOF和△COE中,
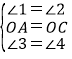
∴△AOF≌△COE(ASA),
∴AF=CE;
(![]() )证明:当旋转角为
)证明:当旋转角为![]() 时,
时,
![]() ,
,
又∵AB⊥AC,
∴∠BAO=90°,
∠AOF=90°,
∴∠BAO=∠AOF,
∴AB∥EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
即:AF∥BE,
∵AB∥EF,AF∥BE,
∴四边形ABEF是平行四边形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.(1)求证:抛物线的对称轴在y轴的左侧;
(2)若
 (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.

(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.
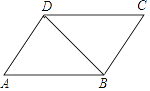
解:∵AD∥CB(已知)
∴∠C+∠ADC=180°(_________________),
又∵∠A=∠C (___________________),
∴∠A+∠ADC=180° (___________________),
∴AB∥CD (___________________________),
∴∠BDC=∠ABD=32° (___________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下说法:①49的平方根是±7,可以记作
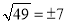 ;②如果一个数的立方根是这个数本身,那么这个数必是1和0;③开方开不尽的数是无理数;④任意一个无理数的绝对值是正数:⑤无理数与有理数的和一定还是无理数.其中正确的有( )
;②如果一个数的立方根是这个数本身,那么这个数必是1和0;③开方开不尽的数是无理数;④任意一个无理数的绝对值是正数:⑤无理数与有理数的和一定还是无理数.其中正确的有( )A. ②③⑤ B. ②③④ C. ①②③ D. ④⑤
-
科目: 来源: 题型:
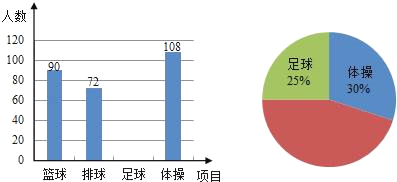
查看答案和解析>>【题目】某中学进行体育教学改革,同时开设篮球、排球、足球、体操课、学生可根据自己的爱好任选其一,体育老师根据七年级学生的报名情况进行了统计,并绘制了下面尚未完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
(1)该校七年级共有多少名学生?
(2)将两个统计图补充完整;
(3)从统计图中你还能得到哪些信息?(写出两条即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°,
(1)求证;BF∥DE.
(2)如果DE⊥AC于点E,∠2=150°,求∠AFG的度数.

相关试题

