【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
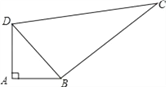
(1)试判断△BCD的形状;
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
参考答案:
【答案】(1)△BCD是直角三角形;理由见解析;(2)学校需要投入7200元买草皮.
【解析】试题分析:连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.
试题解析:(1)△BCD是直角三角形;理由如下:
∵∠A=90°,AB=3,AD=4,BC=12,
根据勾股定理得BD2=AB2+AD2=32+42=25,
∴BD2+BC2=25+144=169=132=CD2,
根据勾股定理的逆定理,∴∠CBD=90°
∴△BCD是直角三角形.
(2)四边形ABCD的面积=S△ABD+S△BCD=![]() ×3×4+
×3×4+![]() ×5×12=6+30=36m2,
×5×12=6+30=36m2,
∴学校要投入资金为:200×36=7200元;
答:学校需要投入7200元买草皮.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益Z(元)会相应降低且Z与x之间也大致满足如图②所示的一次函数关系。

(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
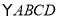 的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式一定成立的是( )
A.x+2<x+3
B.5a>4a
C.﹣a>﹣2a
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简-[-(+43)]=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式1﹣
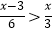 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. 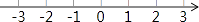
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x、y的二元一次方程组
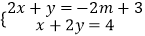 的解满足x﹣y>﹣8.
的解满足x﹣y>﹣8.
(1)用含m的代数式表示x﹣y.
(2)求满足条件的m的所有正整数值.
相关试题

