【题目】如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
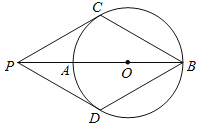
A.4个 B.3个 C.2个 D.1个
参考答案:
【答案】A.
【解析】
试题分析:(1)连接CO,DO,∵PC与⊙O相切,切点为C,∴∠PCO=90°,在△PCO和△PDO中,∵CO=DO,PO=PO,PC=PD,∴△PCO≌△PDO(SSS),∴∠PCO=∠PDO=90°,∴PD与⊙O相切,故(1)正确;
(2)由(1)得:∠CPB=∠BPD,在△CPB和△DPB中,∵PC=PD∠CPB=∠DPB,PB=PB,∴△CPB≌△DPB(SAS),∴BC=BD,∴PC=PD=BC=BD,∴四边形PCBD是菱形,故(2)正确;
(3)连接AC,∵PC=CB,∴∠CPB=∠CBP,∵AB是⊙O直径,∴∠ACB=90°,在△PCO和△BCA中,∵∠CPO=∠CBP,PC=BC,∠PCO=∠BCA,∴△PCO≌△BCA(ASA),∴AC=CO,∴AC=CO=AO,∴∠COA=60°,∴∠CPO=30°,∴CO=![]() PO=
PO=![]() AB,∴PO=AB,故(3)正确;
AB,∴PO=AB,故(3)正确;
(4)∵四边形PCBD是菱形,∠CPO=30°,∴DP=DB,则∠DPB=∠DBP=30°,∴∠PDB=120°,故(4)正确;
正确个数有4个,故选A.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
(1)求证:△CDE≌△CBF;
(2)当DE=
 时,求CG的长;
时,求CG的长;(3)连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应括号里:
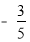 ,8.2,-7,0,-0.3,102 ,-2.1010010001…,
,8.2,-7,0,-0.3,102 ,-2.1010010001…,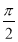 ,
,
非负整数集合:{ …}
分数集合:{ …}
无理数集合:{ …}
负数集合:{ …}
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(1.6)+(- 2.7)+(- 2.3)+2.7
(2)
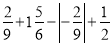
(3)-2+(-2)×3-(-8)
(4)(-24)×(-
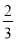 +
+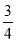 -
-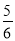 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(2,2)是双曲线
 上一点,点B是双曲线上位于点A右下方的另一点,C是x轴上的点,且△ABC是以∠B为直角的等腰直角三角形,则点B的坐标是__________。
上一点,点B是双曲线上位于点A右下方的另一点,C是x轴上的点,且△ABC是以∠B为直角的等腰直角三角形,则点B的坐标是__________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
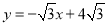 与x轴相交于点A,与直线
与x轴相交于点A,与直线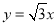 相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为_________________。
相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为_________________。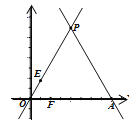
相关试题

