搜索
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1）、P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且﹣1＜x1＜x2，x3＜﹣1，则y1、y2、y3的大小关系为（ ）
A. y1＜y2＜y3 B. y3＜y1＜y2 C. y3＜y2＜y1 D. y2＜y1＜y3
参考答案：
【答案】D
【解析】因为抛物线的对称轴为直线x=-1，开口向下，P1（x1，y1），P2（x2，y2）是抛物线上的点，且-1＜x1＜x2，根据二次函数的性质：在对称轴的右侧，y随x的增大而减小，可得y2＜ y1；P3（x3，y3）是直线l上的点，直线y随x的增大而减小，且x3＜-1，由图象可知，直线上x3对应的函数值y3大于-1对应的函数值，又因x=-1时，抛物线的顶点最高，可得y3最大，所以y2＜y1＜ y3．故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面运用加法结合律的式子是( )
A. 45－76＝－46＋75B. 63－128－72＝63＋(－128－72)
C. 128－75－45＝128－(75+45)D. a＋b＋c＝b＋a＋c
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG =BD，连接BG、DF．若AF=8，CF=6，求四边形BDFG的周长.
-
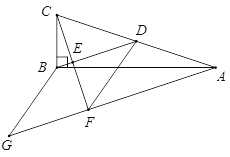
科目： 来源： 题型：
查看答案和解析>>【题目】《列子》中《歧路亡羊》写道：
杨子之邻人亡羊，既率其党，又请杨子之竖追之。杨 子曰：“嘻!亡一羊，何追者之众?”邻人日：“多歧路。”既 反，问：“获羊乎?”日：“亡之矣。”曰：“奚亡之?”曰：“歧路 之中又有歧焉，吾不知所之，所以反也.”
如图，假定所有的分叉口都各有两条新的歧路，并且丢失的羊走每条歧路的可能性都相等.
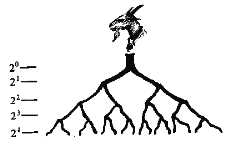
（1）到第n次分歧时，共有多少条歧路？以当羊走过n个三叉路口后，找到羊的概率是多少？
（2）当n=5时，派出6个人去找羊，找到羊的概率是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，线段AB的两个端点分别为A(2，3)，B(-1，2).将线段AB通过平移后得到线段A′B′，若A的对应点为A′(7，6)，则B的对应点B′的坐标是________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明根据下列模型,分别画出了三视图,他画的是否都正确?如果有不正确的,请你帮助修改一下(箭头表示主视方向).
(1)
(2)
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
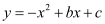经过点A（3，0），B（－1，0）．（1）求抛物线的解析式；
（2）求抛物线的顶点坐标．
相关试题
