【题目】如图,直线x=﹣4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=﹣4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.
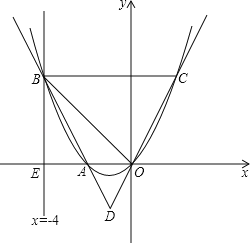
(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式.
参考答案:
【答案】(1)(﹣2,0);(2)y=![]() x2+
x2+![]() x或y=
x或y=![]() x2+
x2+![]() x.
x.
【解析】
试题分析:(1)过点D作DF⊥x轴于点F,由抛物线的对称性可知OF=AF,则2AF+AE=4①,由DF∥BE,得到△ADF∽△ABE,根据相似三角形对应边成比例得出![]() =
=![]() ,即AE=2AF②,①与②联立组成二元一次方程组,解出AE=2,AF=1,进而得到点A的坐标;
,即AE=2AF②,①与②联立组成二元一次方程组,解出AE=2,AF=1,进而得到点A的坐标;
(2)先由抛物线过原点(0,0),设此抛物线的解析式为y=ax2+bx,再根据抛物线过原点(0,0)和A点(﹣2,0),求出对称轴为直线x=﹣1,则由B点横坐标为﹣4得出C点横坐标为2,BC=6.再由OB>OC,可知当△OBC是等腰三角形时,可分两种情况讨论:①当OB=BC时,设B(﹣4,y1),列出方程,解方程求出y1的值,将A,B两点坐标代入y=ax2+bx,运用待定系数法求出此抛物线的解析式;②当OC=BC时,设C(2,y2),列出方程,解方程求出y2的值,将A,C两点坐标代入y=ax2+bx,运用待定系数法求出此抛物线的解析式.
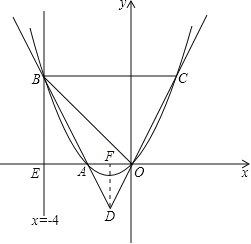
试题解析:(1)如图,过点D作DF⊥x轴于点F.
由题意,可知OF=AF,则2AF+AE=4①.
∵DF∥BE,
∴△ADF∽△ABE,
∴![]() =
=![]() ,即AE=2AF②,
,即AE=2AF②,
①与②联立,解得AE=2,AF=1,
∴点A的坐标为(﹣2,0);
(2)∵抛物线过原点(0,0),
∴可设此抛物线的解析式为y=ax2+bx.
∵抛物线过原点(0,0)和A点(﹣2,0),
∴对称轴为直线x=![]() =﹣1,
=﹣1,
∵B、C两点关于直线x=﹣1对称,B点横坐标为﹣4,
∴C点横坐标为2,
∴BC=2﹣(﹣4)=6.
∵抛物线开口向上,
∴∠OAB>90°,OB>AB=OC,
∴当△OBC是等腰三角形时,分两种情况讨论:
①当OB=BC时,设B(﹣4,y1),
则16+![]() =36,解得y1=±2
=36,解得y1=±2![]() (负值舍去).
(负值舍去).
将A(﹣2,0),B(﹣4,2![]() )代入y=ax2+bx,
)代入y=ax2+bx,
得![]() ,解得
,解得![]() .
.
∴此抛物线的解析式为y=![]() x2+
x2+![]() x;
x;
②当OC=BC时,设C(2,y2),
则4+![]() =36,解得y2=±4
=36,解得y2=±4![]() (负值舍去).
(负值舍去).
将A(﹣2,0),C(2,4![]() )代入y=ax2+bx,
)代入y=ax2+bx,
得![]() ,解得
,解得![]() .
.
∴此抛物线的解析式为y=![]() x2+
x2+![]() x.
x.
综上可知,若△OBC是等腰三角形,此抛物线的函数关系式为y=![]() x2+
x2+![]() x或y=
x或y=![]() x2+
x2+![]() x.
x.
-
科目: 来源: 题型:
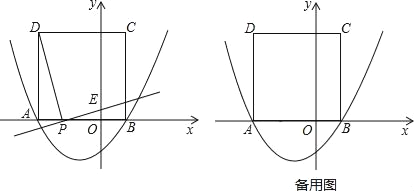
查看答案和解析>>【题目】如图,已知二次函数y=
 x2+bx﹣
x2+bx﹣ 与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.(1)试求出二次函数的表达式和点B的坐标;
(2)当点P在线段AO(点P不与A、O重合)运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由.
(2)求∠DBE的度数.
(3)若把AD左右平行移动,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出此时∠ADB的度数;若不存在,请说明理由.

-
科目: 来源: 题型:
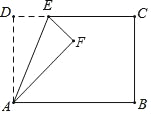
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:x2﹣2(x2﹣3xy)+3(y2﹣2xy)﹣2y2,其中x=
 ,y=﹣1;
,y=﹣1;(2)已知x+y=6,xy=﹣1,求代数式2(x+1)﹣(3xy﹣2y)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
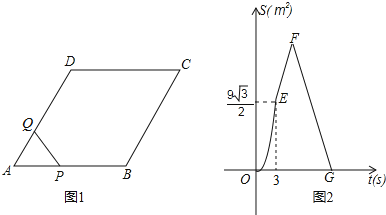
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置;

(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
相关试题

