【题目】在平面直角坐标系中,已知点A(4,0)、B(-6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为 .
参考答案:
【答案】(0,12)或(0,-12).
【解析】试题解析:设线段BA的中点为E,
∵点A(4,0)、B(-6,0),∴AB=10,E(-1,0).
(1)如图1所示,过点E在第二象限作EP⊥BA,且EP=![]() AB=5,
AB=5,
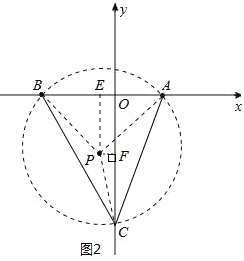
则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=![]() ;
;
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=![]() ∠BPA=45°,即则点C即为所求.
∠BPA=45°,即则点C即为所求.
过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,
在Rt△PFC中,PF=1,PC=![]() ,由勾股定理得:CF=
,由勾股定理得:CF=![]() =7,
=7,
∴OC=OF+CF=5+7=12,
∴点C坐标为(0,12);
(2)如图2所示,在第3象限可以参照(1)作同样操作,

同理求得y轴负半轴上的点C坐标为(0,-12).
综上所述,点C坐标为(0,12)或(0,-12).
-
科目: 来源: 题型:
查看答案和解析>>【题目】试解答下列问题:
(1)在图1我们称之为“8字形”,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3) 在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .

-
科目: 来源: 题型:
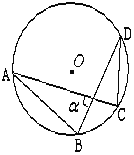
查看答案和解析>>【题目】如图⊙O的半径为1cm,弦AB、CD的长度分别为
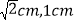 ,则弦AC、BD所夹的锐角
,则弦AC、BD所夹的锐角 = .
= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,EF过对角线的交点,若AB=4,BC=7,OE=1.5,则四边形EFDC的周长是( )

A. 14B. 17C. 10D. 11
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 ,结论:①
,结论:① ;②
;② ;③
;③ ;④
;④ ,其中正确的是有( )
,其中正确的是有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.
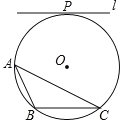
(1)仅用无刻度的直尺,画出一条弦,使这条炫将△ABC分成面积相等的两部分(保留作图痕迹,不写画法).
(2)求弦BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是平行四边形,AC、BD交于点O,∠1=∠2.
(1)求证:四边形ABCD是矩形;(2)若∠BOC=120°,AB=4cm,求四边形ABCD的面积.

相关试题

