【题目】如图,二次函数y=ax2+bx+c(a≠0)的大致图象,关于该二次函数下列说法正确的是( )

A. a>0,b<0,c>0
B. b2﹣4ac<0
C. 当﹣1<x<2时,y>0
D. 当x>2时,y随x的增大而增大
参考答案:
【答案】D
【解析】试题分析:由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,于是可对A选项进行判断;根据抛物线与x轴的交点个数可对B选项进行判断;根据函数图象,利用函数图象在x轴上方所对应的自变量的取值范围对C选项进行判断;根据二次函数的增减性可对D选项进行判断.
解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,所以A选项错误;
∵抛物线与x轴有2个交点,
∴△=b24ac>0,所以B选项错误;
∵抛物线与x轴交于点(1,0)、(2,0),
∴当1<x<2时,y<0,所以C选项错误;
∵x>2在对称轴的右侧,
∴y随x的增大而增大,所以D选项正确。
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.
x
…
﹣1
0
1
2
3
…
y
…
b
1
0
1
2
…
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .

-
科目: 来源: 题型:
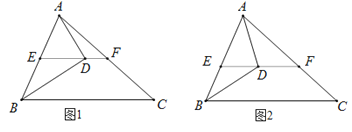
查看答案和解析>>【题目】如图,在△ABC中,点D为∠ABC的平分线BD上一点,连接AD,过点D作EF∥BC交AB于点E,交AC于点F.
(1)如图1,若AD⊥BD于点D,∠BEF=130°,求∠BAD的度数;
(2)如图2,若∠ABC=α,∠BDA=β,求∠FAD+∠C的度数(用含α和β的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】蚂蚁森林是支付宝客户端为首期"碳账户"设计的一款公益行动:用户如果步行、地铁出行、在线缴纳水电煤气费、网上缴交通罚单、网络挂号、网络购票等行为,就会减少相应的碳排放量,可以用来在支付宝里养一棵虚拟的树.这棵树长大后,公益组织、环保企业等蚂蚁生态伙伴们,可以“买走”用户的“树”,而在现实某个地域种下一棵实体的树.为了响应支付宝蚂蚁森林活动,某健身器材销售公司捐出五月份全部销售利润用于买“树”、种树.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款64万元和其他各项支出(人员工资和杂项开支)3.8万元.这三种器材的进价和售价如下表,人员工资(万元)和杂项支出(万元)分别与总销售量x(台)成一次函数关系(如图).


(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利润为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
(4)请推测该公司这次活动捐款金额的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列二次函数中有一个函数的图像与x轴有两个不同的交点,这个函数是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
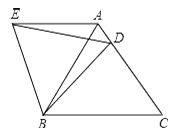
查看答案和解析>>【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是__(把你认为正确结论的序号都填上.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点中,位于平面直角坐标系第四象限的点是( )
A. (1,2) B. (﹣1,2) C. (1,﹣2) D. (﹣1,﹣2)
相关试题

