【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( ) 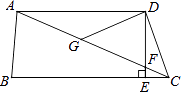
A.2 ![]()
B.![]()
C.2 ![]()
D.![]()
参考答案:
【答案】C
【解析】解:∵AD∥BC,DE⊥BC, ∴DE⊥AD,∠CAD=∠ACB,∠ADE=∠BED=90°,
又∵点G为AF的中点,
∴DG=AG,
∴∠GAD=∠GDA,
∴∠CGD=2∠CAD,
∵∠ACD=2∠ACB=2∠CAD,
∴∠ACD=∠CGD,
∴CD=DG=3,
在Rt△CED中,DE= ![]() =2
=2 ![]() .
.
故选:C.
根据直角三角形斜边上的中线的性质可得DG=AG,根据等腰三角形的性质可得∠GAD=∠GDA,根据三角形外角的性质可得∠CGD=2∠GAD,再根据平行线的性质和等量关系可得∠ACD=∠CGD,根据等腰三角形的性质可得CD=DG,再根据勾股定理即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春季是流行性感冒高发的季节.某种感冒病毒的直径是0.00000002019米,数据0.00000002019用科学记数法可表示为_____.
-
科目: 来源: 题型:
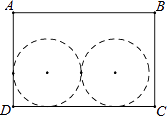
查看答案和解析>>【题目】如图,长方形ABCD的面积为300cm2 , 长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A=4x2﹣3x﹣2,B=4x2﹣3x﹣4,则A,B的大小关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=
 ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)= .
.(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点E为射线BC上一点,∠B+∠DCB=180°,连接ED,过点A的直线MN∥ED.
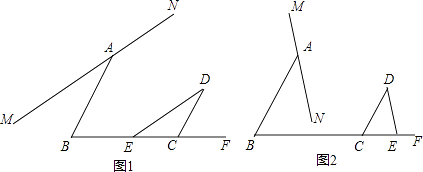
(1)如图1,当点E在线段BC上时,猜想并验证∠MAB=∠CDE.
(2)如图2,当点E在线段BC的延长线时,猜想并验证∠MAB与∠CDE的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】第六次全国人口普查公布的数据表明,登记的全国人靠数量约为1 340 000 000人.这个数据用科学记数法表示为( )
A、134×107人B、13.4×108人
C、1.34×109人D、1.34×1010人
相关试题

