【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C 
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:令y=0得﹣ ![]() x2﹣
x2﹣ ![]() x+2=0,
x+2=0,
∴x2+2x﹣8=0,
x=﹣4或2,
∴点A坐标(2,0),点B坐标(﹣4,0),
令x=0,得y=2,
∴点C坐标(0,2)
(2)
解:由图象可知AB只能为平行四边形的边,
∵AB=EF=6,对称轴x=﹣1,
∴点E的横坐标为﹣7或5,
∴点E坐标(﹣7,﹣ ![]() )或(5,﹣
)或(5,﹣ ![]() ),此时点F(﹣1,﹣
),此时点F(﹣1,﹣ ![]() ),∴以A,B,E,F为顶点的平行四边形的面积=6×
),∴以A,B,E,F为顶点的平行四边形的面积=6× ![]() =
= ![]()
(3)
如图所示,

①当C为顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,
在RT△CM1N中,CN= ![]() =
= ![]() ,
,
∴点M1坐标(﹣1,2+ ![]() ),点M2坐标(﹣1,2﹣
),点M2坐标(﹣1,2﹣ ![]() ).
).
②当M3为顶点时,∵直线AC解析式为y=﹣x+1,
线段AC的垂直平分线为y=x,
∴点M3坐标为(﹣1,﹣1).
③当点A为顶点的等腰三角形不存在.
综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+ ![]() )或(﹣1.2﹣
)或(﹣1.2﹣ ![]() ).
).
【解析】(1)分别令y=0,x=0,即可解决问题.(2)由图象可知AB只能为平行四边形的边,易知点E坐标(﹣7,﹣ ![]() )或(5,﹣
)或(5,﹣ ![]() ),由此不难解决问题.(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.本题考查二次函数综合题、平行四边形的判定和性质、勾股定理等知识,解题的关键是熟练掌握抛物线与坐标轴交点的求法,学会分类讨论的思想,属于中考压轴题.
),由此不难解决问题.(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.本题考查二次函数综合题、平行四边形的判定和性质、勾股定理等知识,解题的关键是熟练掌握抛物线与坐标轴交点的求法,学会分类讨论的思想,属于中考压轴题.
【考点精析】根据题目的已知条件,利用勾股定理的概念和平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
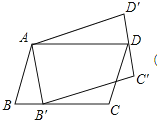
查看答案和解析>>【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有个

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
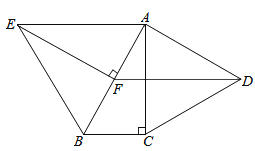
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.

(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.
①如图1,若∠MON=150°,求证:△ABR为等边三角形;
②如图3,若△ARB∽△PEQ,求∠MON大小和 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.

(1)当E为BC中点时,求证:△BCF≌△DEC;
(2)当BE=2EC时,求 的值;
的值;
(3)设CE=1,BE=n,作点C关于DE的对称点C′,连结FC′,AF,若点C′到AF的距离是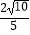 ,求n的值.
,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )

A.2
B.2.4
C.2.6
D.3
相关试题

