【题目】已知甲同学手中藏有三张分别标有数字![]() ,
,![]() ,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果.
(2)现制定这样一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释.
参考答案:
【答案】(1)见解析;(2)不公平
【解析】(1)首先根据题意画出树状图,然后根据树状图即可求得所有等可能的结果;
(2)利用一元二次方程根的判别式,即可判定各种情况下根的情况,然后利用概率公式求解即可求得甲、乙获胜的概率,比较概率大小,即可确定这样的游戏规是否公平.
解:(1)画树状图得:
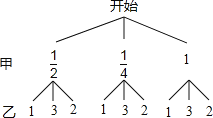
∵(a,b)的可能结果有(![]() ,1)、(
,1)、(![]() ,3)、(
,3)、(![]() ,2)、(
,2)、(![]() ,1)、(
,1)、(![]() ,3)、(
,3)、(![]() ,2)、(1,1)、(1,3)及(1,2),
,2)、(1,1)、(1,3)及(1,2),
∴(a,b)取值结果共有9种;
(2)∵当a=![]() ,b=1时,△=b2-4ac=-1<0,此时ax2+bx+1=0无实数根,
,b=1时,△=b2-4ac=-1<0,此时ax2+bx+1=0无实数根,
当a=![]() ,b=3时,△=b2-4ac=7>0,此时ax2+bx+1=0有两个不相等的实数根,
,b=3时,△=b2-4ac=7>0,此时ax2+bx+1=0有两个不相等的实数根,
当a=![]() ,b=2时,△=b2-4ac=2>0,此时ax2+bx+1=0有两个不相等的实数根,
,b=2时,△=b2-4ac=2>0,此时ax2+bx+1=0有两个不相等的实数根,
当a=![]() ,b=1时,△=b2-4ac=0,此时ax2+bx+1=0有两个相等的实数根,
,b=1时,△=b2-4ac=0,此时ax2+bx+1=0有两个相等的实数根,
当a=![]() ,b=3时,△=b2-4ac=8>0,此时ax2+bx+1=0有两个不相等的实数根,
,b=3时,△=b2-4ac=8>0,此时ax2+bx+1=0有两个不相等的实数根,
当a=![]() ,b=2时,△=b2-4ac=3>0,此时ax2+bx+1=0有两个不相等的实数根,
,b=2时,△=b2-4ac=3>0,此时ax2+bx+1=0有两个不相等的实数根,
当a=1,b=1时,△=b2-4ac=-3<0,此时ax2+bx+1=0无实数根,
当a=1,b=3时,△=b2-4ac=5>0,此时ax2+bx+1=0有两个不相等的实数根,
当a=1,b=2时,△=b2-4ac=0,此时ax2+bx+1=0有两个相等的实数根,
∴P(甲获胜)=P(△>0)=![]() >P(乙获胜)=
>P(乙获胜)=![]() ,
,
∴这样的游戏规则对甲有利,不公平.
“点睛”本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
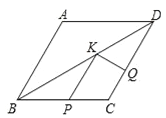
A. 1 B.
 C. 2 D.
C. 2 D.  +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】用式子表示“a的平方与1的差”: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式22a2b的系数和次数分别是( )
A.2,2
B.4,5
C.2,3
D.4,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.
(1)设花圃的一边AB长为x米,请你用含x的代数式表示另一边AD的长为 米;
(2)若此时花圃的面积刚好为45m2,求此时花圃的长与宽.

-
科目: 来源: 题型:
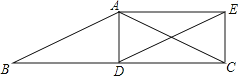
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
(1)求证:△ACD≌△EDC;
(2)若点D是BC中点,说明四边形ADCE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△DEF,∠A=80°,∠B=60°,∠C=40°,则∠E=_________°.
相关试题

