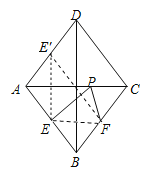
【题目】如图,菱形ABCD中,AB=4,E,F分别是AB、BC的中点,P是AC上一动点,则PF+PE的最小值是( )

A. 3B. ![]() C. 4D.
C. 4D. ![]()
参考答案:
【答案】C
【解析】
作点E关于AC的对称点E',连接E'F与AC交点为P点,此时EP+PF的值最小;易求E'是AD的中点,证得四边形ABF E'是平行四边形,所以E'F=AB=4,即PF+PE的最小值是4.
作点E关于AC的对称点E',连接E'F,与AC交点为P点,此时EP+PF的值最小;
连接EF,
∵菱形ABCD,
∴AC⊥BD
∵E,F分别是边AB,BC的中点,
∴E'是AD的中点,
∴A E'=![]() AD,BF=
AD,BF=![]() BC,E'E⊥EF,
BC,E'E⊥EF,
∵菱形ABCD,
∴AD=BC,AD∥BC,
∴A E'=BF,A E'∥BF,
∴四边形ABF E'是平行四边形,
∴E'F=AB=4,
即PF+PE的最小值是4.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,最适合使用全面调查的方式收集数据的是( )
A.了解某地区人民对修建高速路的意见
B.了解同批次
 灯泡的使用寿命
灯泡的使用寿命C.了解我校七年级某班同学的课外阅读时间
D.了解昆明市中学生对“社会主义核心价值观”的知晓率
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生对数学知识的理解和应用,某校学生会专门针对七年级举办了“数学知识应用创新能力”测试,七年级的所有学生都参加了测试,试卷共有
 道题,每题
道题,每题 分.测试结束后随机抽取了部分学生的测试成绩绘制出部分频数分布表和频数分布直方图,请结合图表完成下列各题:
分.测试结束后随机抽取了部分学生的测试成绩绘制出部分频数分布表和频数分布直方图,请结合图表完成下列各题:组别
成绩
 分
分频数(人数)
第
 组
组

第
 组
组

第
 组
组
第
 组
组

第
 组
组

合计


(
 )频数分布表中
)频数分布表中 的值等于 ;
的值等于 ;(
 )请把频数分布直方图补充完整;
)请把频数分布直方图补充完整;(
 )若测试成绩不低于
)若测试成绩不低于 分为优秀,请你估计七年级
分为优秀,请你估计七年级 名学生成绩优秀的有多少人?
名学生成绩优秀的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E为BC上一点,BE=2CE,连接DE,F为DE中点,以DF为直角边作等腰Rt△DFG,连接BG,将△DFG绕点D顺时针旋转得△DF′G′,G′恰好落在BG的延长线上,连接F′G,若BG=2
 ,则S△GF′G′=________.
,则S△GF′G′=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强对校内外的安全监控,创建平安校园,某学校计划增加
 台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如表所示,经调查,购买
台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如表所示,经调查,购买 台甲型设备比购买
台甲型设备比购买 台乙型设备少
台乙型设备少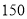 元,购买
元,购买 台甲型设备比购买
台甲型设备比购买 台乙型设备多
台乙型设备多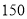 元.
元.甲型
乙型
价格(元/台)


有效半径(米/台)

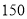
(
 )求
)求 ,
, 的值;
的值;(
 )若购买该批设备的资金不超过
)若购买该批设备的资金不超过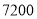 元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?(
 )在(
)在( )的条件下,若要求监控半径覆盖范围不低于
)的条件下,若要求监控半径覆盖范围不低于 米,为了节约资金,请你设计一种最省钱的购买方案.
米,为了节约资金,请你设计一种最省钱的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某网络公司员工月收人情况表.
月收入(元)








人数








(1)求此公司员工月收人的中位数;
(2)小张求出这个公司员工月收人平均数为
 元,若用所求平均数反映公司全体员工月收人水平,合适吗?若不合适,用什么数据更好?
元,若用所求平均数反映公司全体员工月收人水平,合适吗?若不合适,用什么数据更好? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知王亮家、公园、新华书店在一条直线上,下面的图象反映的过程是:王亮从家跑步去公园,在那里锻炼了一阵后又走到新华书店去买书,然后散步走回家.其中
 表示时间,
表示时间, 表示王亮离家的距离.
表示王亮离家的距离.
根据图象回答:
(1)公园离王亮家
 ,王亮从家到公园用了
,王亮从家到公园用了  ;
;(2)公园离新华书店
 ;
;(3)王亮在新华书店逗留了
 ;
;(4)王亮从新华书店回家的平均速度是多少?
相关试题

