【题目】如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为 . 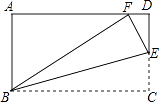
参考答案:
【答案】![]()
【解析】解:设CE=x. ∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=3,∠A=∠D=90°.
∵将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,
∴BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.
在Rt△ABF中,由勾股定理得:
AF2=52﹣32=16,
∴AF=4,DF=5﹣4=1.
在Rt△DEF中,由勾股定理得:
EF2=DE2+DF2 ,
即x2=(3﹣x)2+12 ,
解得:x= ![]() ,
,
故答案为 ![]() .
.
设CE=x,由矩形的性质得出AD=BC=5,CD=AB=3,∠A=∠D=90°.由折叠的性质得出BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.在Rt△ABF中利用勾股定理求出AF的长度,进而求出DF的长度;然后在Rt△DEF根据勾股定理列出关于x的方程即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=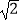 .
.
其中正确的结论有( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
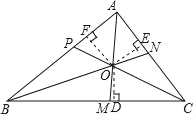
查看答案和解析>>【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=
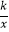 (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
②k=4;
③当0<x<2时,y1<y2;
④如图,当x=4时,EF=4.
其中正确结论的个数是( )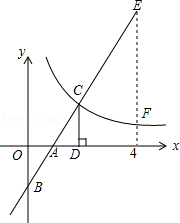
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
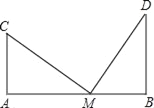
查看答案和解析>>【题目】如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0、5m/s,求这个人走了多长时间?
-
科目: 来源: 题型:
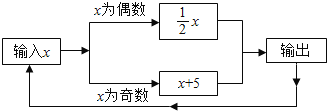
查看答案和解析>>【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2017次输出的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的条形统计图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
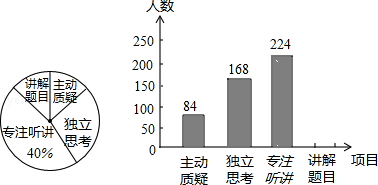
(1)在这次评价中,一共抽查了名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;
(3)请将条形统计图补充完整;
(4)如果全市有6000名九年级学生,那么在试卷评讲课中,“独立思考”的约有多少人?
相关试题

