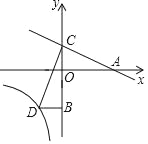
【题目】如图,直线y=kx+b过点A(5,0)和点C,反比例函数y=![]() (x<0)过点D,作BD∥x轴交y轴于点B(0,﹣3),且BD=OC,tan∠OAC=
(x<0)过点D,作BD∥x轴交y轴于点B(0,﹣3),且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() (x<0)和直线y=kx+b的解析式;
(x<0)和直线y=kx+b的解析式;
(2)连接CD,判断线段AC与线段CD的关系,并说明理由.
参考答案:
【答案】(1)y=![]() ,y=﹣
,y=﹣![]() x+2;(2)AC⊥CD.
x+2;(2)AC⊥CD.
【解析】分析:(1)由A点坐标可求得OA的长,再利用三角函数的定义可求得OC的长,可求得C、D点坐标,再利用待定系数法可求得直线AC的解析式;
(2)由条件可证明△OAC≌△BCD,再由角的和差可求得∠OAC+∠BCA=90°,可证得AC⊥CD.
详解:(1)∵A(5,0),∴OA=5.
∵tan∠OAC=![]() =
=![]() .
.
解得:OC=2,∴C(0,2),∴BD=OC=2.
∵B(0,﹣3),BD∥x轴,∴D(﹣2,﹣3),∴m=﹣2×(﹣3)=6,∴y=![]() .
.
设直线AC关系式为y=kx+b.
∵过A(5,0),C(0,2),∴![]() ,
,
解得: ,∴y=﹣
,∴y=﹣![]() +2;
+2;
(2)∵B(0,﹣3),C(0,2),∴BC=5=OA.
∵x轴⊥y轴,∠AOC=∠COE=90°,BD∥x轴,
∴∠COE=∠DBC=90°,∴∠AOC=∠DBC.
在△OAC和△BCD中,
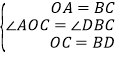
∴△OAC≌△BCD(SAS),
∴AC=CD,∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD.

-
科目: 来源: 题型:
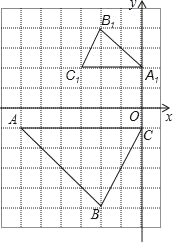
查看答案和解析>>【题目】如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC 的位置如图所示:(每个小方格都是边长为 1 个单位长度的正方形)
(1)将△ABC 沿 y 轴方向向下平移 4 个单位长度得到
 则点
则点  坐标为_______;
坐标为_______;(2)将△ABC 绕着点 O 逆时针旋转 90°,画出旋转后得到的
 ;
;(3)直接写出点
 ,
, 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元.小王携带现金3 000元到该市场采购苹果,并以批发价买进.如果购进的苹果是x千克,小王付款后剩余现金y元.
(1)试写出x与y之间的函数关系式,并指出自变量的取值范围;
(2)画出函数图象,指出图象形状和终点坐标;
(3)若小王以每千克3元的价格将苹果卖出,卖出x千克后可获利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, ABCD 的对角线 AC 、 BD 相交于点O , BD 12cm , AC 6cm ,点 E 在线段 BO 上从点 B 以1cm / s 的速度向点 O 运动,点 F 在线段OD 上从点O 以 2cm / s 的速度向点 D 运动.
(1)若点 E 、F 同时运动,设运动时间为t 秒,当t 为何值时,四边形 AECF 是平行四边形.
(2)在(1)的条件下,当 AB 为何值时, AECF 是菱形;
(3)求(2)中菱形 AECF 的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
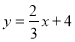 与
与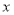 轴、
轴、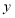 轴分别交于点
轴分别交于点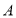 和点
和点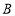 ,点
,点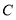 ,
,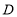 分别为线段
分别为线段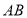 ,
,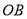 的中点,点
的中点,点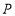 为
为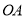 上一动点,
上一动点,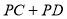 值最小时,点
值最小时,点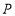 的坐标为______.
的坐标为______.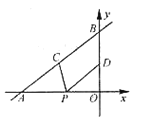
相关试题

