【题目】定义:我们把三角形被一边中线分成的两个三角形叫做“朋友三角形”.
性质:“朋友三角形”的面积相等.
如图1,在△ABC中,CD是AB边上的中线.
那么△ACD和△BCD是“朋友三角形”,并且S△ACD=S△BCD .
应用:如图2,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=AD=4,BC=6,点E在BC上,点F在AD上,BE=AF,AE与BF交于点O.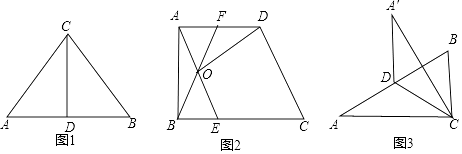
(1)求证:△AOB和△AOF是“朋友三角形”;
(2)连接OD,若△AOF和△DOF是“朋友三角形”,求四边形CDOE的面积.
拓展:如图3,在△ABC中,∠A=30°,AB=8,点D在线段AB上,连接CD,△ACD和△BCD是“朋友三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的 ![]() ,则△ABC的面积是(请直接写出答案).
,则△ABC的面积是(请直接写出答案).
参考答案:
【答案】
(1)
证明:∵AD∥BC,
∴∠OAF=∠OEB,
在△AOF和△EOB中, 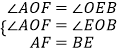 ,
,
∴△AOF≌△EOB(AAS),
∴OF=OB,
则AO是△ABF的中线.
∴△AOB和△AOF是“朋友三角形”
(2)8或8 ![]()
【解析】(2)解:∵△AOF和△DOF是“朋友三角形”,
∴S△AOF=S△DOF ,
∵△AOF≌△EOB,
∴S△AOB=S△EOB ,
∵△AOB和△AOF是“朋友三角形”
∴S△AOB=S△AOF ,
∴S△AOF=S△DOF=S△AOB=S△EOB , = ![]() ×4×2=4,
×4×2=4,
∴四边形CDOE 的面积=S梯形ABCD﹣2S△ABE= ![]() ×(4+6)×4﹣2×4=12;
×(4+6)×4﹣2×4=12;
拓展:解:分为两种情况:①如图1所示:
∵S△ACD=S△BCD .
∴AD=BD= ![]() AB=4,
AB=4,
∵沿CD折叠A和A′重合,
∴AD=A′D= ![]() AB=
AB= ![]() ×8=4,
×8=4,
∵△A′CD与△ABC重合部分的面积等于△ABC面积的 ![]() ,
,
∴S△DOC= ![]() S△ABC=
S△ABC= ![]() S△BDC=
S△BDC= ![]() S△ADC=
S△ADC= ![]() S△A′DC ,
S△A′DC ,
∴DO=OB,A′O=CO,
∴四边形A′DCB是平行四边形,
∴BC=A′D=4,
过B作BM⊥AC于M,
∵AB=8,∠BAC=30°,
∴BM= ![]() AB=4=BC,
AB=4=BC,
即C和M重合,
∴∠ACB=90°,由勾股定理得:AC= ![]() =4
=4 ![]() ,
,
∴△ABC的面积= ![]() ×BC×AC=
×BC×AC= ![]() ×4×4
×4×4 ![]() =8
=8 ![]() ;
;
②如图2所示:
∵S△ACD=S△BCD .
∴AD=BD= ![]() AB,
AB,
∵沿CD折叠A和A′重合,
∴AD=A′D= ![]() AB=
AB= ![]() ×8=4,
×8=4,
∵△A′CD与△ABC重合部分的面积等于△ABC面积的 ![]() ,
,
∴S△DOC= ![]() S△ABC=
S△ABC= ![]() S△BDC=
S△BDC= ![]() S△ADC=
S△ADC= ![]() S△A′DC ,
S△A′DC ,
∴DO=OA′,BO=CO,
∴四边形A′BDC是平行四边形,
∴A′C=BD=4,
过C作CQ⊥A′D于Q,
∵A′C=4,∠DA′C=∠BAC=30°,
∴CQ= ![]() A′C=2,
A′C=2,
∴S△ABC=2S△ADC=2S△A′DC=2× ![]() ×A′D×CQ=2×
×A′D×CQ=2× ![]() ×4×2=8;
×4×2=8;
即△ABC的面积是8或8 ![]() ;
;
所以答案是:8或8 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a3=a6B.a6÷a3=a2C.(ab)2=ab2D.(﹣a2)3=﹣a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据给出的数轴及已知条件,解答下面的问题:

(1)已知点A,B,C表示的数分别为1,﹣ ,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M , N;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P , Q(用含m,n的式子表示这两个数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距40km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中CD、OE分别表示甲、乙离开A地的路程y(km)与时间x(h)的函数关系的图象,结合图象解答下列问题.
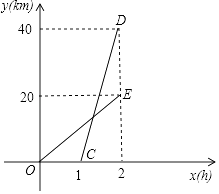
(1)甲比乙晚出发小时,乙的速度是km/h;
(2)在甲出发后几小时,两人相遇?
(3)甲到达B地后,原地休息0.5小时,从B地以原来的速度和路线返回A地,求甲在返回过程中与乙相距10km时,对应x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】文具店老板以每个144元的价格卖出两个计算器,其中一个赚了20%,另一个亏了20%,则卖这两个计算器总的是( )
A. 不赚不赔 B. 亏12元 C. 盈利8元 D. 亏损8元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒
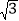 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.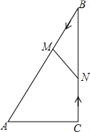
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=
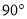 ,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.(1)求证:四边形ECBF是平行四边形;
(2) 当∠A=
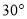 时,求证:四边形ECBF是菱形.
时,求证:四边形ECBF是菱形.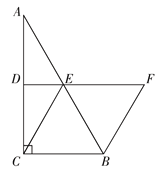
相关试题

