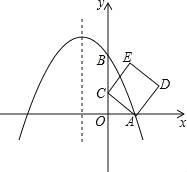
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交于点A(1,0),与y轴交于点B,其对称轴是x=-1,点C是y轴上一点,其纵坐标为m,连结AC,将线段AC绕点A顺时针旋转90°得到线段AD,以AC、AD为边作正方形ACED.
(1)用含m的代数式表示点D的横坐标为 .
(2)求该抛物线所对应的函数表达式.
(3)当点E落在抛物线y=ax2+bx+2上时,求此时m的值.
(4)令抛物线与x轴另一交点为点F,连结BF,直接写出正方形ACED的一边与BF平行时的m的值.
参考答案:
【答案】(1)m+1;(2)y=-![]() x2-
x2-![]() x+2;(3)
x+2;(3)![]() 或
或![]() ;(4)
;(4)![]() 或-
或-![]() .
.
【解析】
试题分析:(1)作DH⊥x轴于H,如图1,先利用等角的余角相等得到∠ACO=∠DAH,则可根据“AAS”证明△ACO≌△DAH,所以AH=OC=m,易得点D的横坐标为m+1;
(2)利用对称轴方程和二次函数图象上点的坐标特征列方程组 ,解方程组求出a和b即可得到抛物线的解析式;
,解方程组求出a和b即可得到抛物线的解析式;
(3)作EG⊥y轴于G,如图1,通过与(1)方法一样证明△ACO≌△CEG得到GE=OC=m,CG=OA=1,则E点坐标为(m,m+1),然后把E点坐标代入(2)中解析式得到关于m的方程,再解方程即可得到m的值;
(4)先通过解方程-![]() x2-
x2-![]() x+2=0得F(-3,0),计算当x=0时的函数值得到B(0,2),讨论:当点C在y轴的正半轴上,即m>0时,如图1,证明△ADH∽△FBO,利用相似比可得到m的值;当点C在y轴的负半轴上,即m<0时,如图2,证明△AOC∽△FOB,利用相似比可计算出m.
x+2=0得F(-3,0),计算当x=0时的函数值得到B(0,2),讨论:当点C在y轴的正半轴上,即m>0时,如图1,证明△ADH∽△FBO,利用相似比可得到m的值;当点C在y轴的负半轴上,即m<0时,如图2,证明△AOC∽△FOB,利用相似比可计算出m.
试题解析:(1)作DH⊥x轴于H,如图1,

∵四边形ADEC为正方形,
∴AC=AD,∠CAD=90°,
∵∠CAO+∠ACO=90°,∠CAO+∠DAH=90°,
∴∠ACO=∠DAH,
在△ACO和△DAH中,
 ,
,
∴△ACO≌△DAH,
∴AH=OC=m,
∴OH=OA+AH=m+1,
∴点D的横坐标为m+1;
(2)根据题意得 ,解得
,解得 ,
,
故抛物线的解析式为y=-![]() x2-
x2-![]() x+2;
x+2;
(3)作EG⊥y轴于G,如图1,
与(1)方法一样可证明得△ACO≌△CEG,则GE=OC=m,CG=OA=1,
∴E点坐标为(m,m+1),
把E(m,m+1)代入y=-![]() x2-
x2-![]() x+2得-
x+2得-![]() m2-
m2-![]() m+2=m+1,
m+2=m+1,
整理得2m2+7m-3=0,解得m1=![]() ,m2=
,m2=![]() ,
,
即m的值为![]() 或
或![]() ;
;
(4)当y=0时,-![]() x2-
x2-![]() x+2=0,解得x1=-3,x2=1,则F(-3,0),
x+2=0,解得x1=-3,x2=1,则F(-3,0),
当x=0时,y=-![]() x2-
x2-![]() x+2=2,则B(0,2),
x+2=2,则B(0,2),
当点C在y轴的正半轴上,即m>0时,如图1,
∵AD∥BF,
∴∠DAH=∠BFO,
∴△ADH∽△FBO,
∴AH:OF=DH:OB,即m:3=1:2,解得m=![]() ;
;
当点C在y轴的负半轴上,即m<0时,如图2,

∵AC∥BF,
∴∠ACO=∠OBF,
∴△AOC∽△FOB,
∴AO:OF=OC:OB,1,即1:3=-m:2,解得m=-![]() ,
,
即m的值为![]() 或-
或-![]() .
.
-
科目: 来源: 题型:
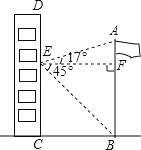
查看答案和解析>>【题目】如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).
【参考数据:sin17°=0.29,cos17°=0.96,tan17°=0.31】
-
科目: 来源: 题型:
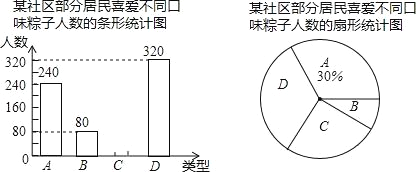
查看答案和解析>>【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,某市食品企业计划在今年推出:海参干贝棕、板栗鲜肉粽、水晶蜜浅粽、咖喱牛肉粽(以下分别用A、B、C、D表示)四种口味的粽子.该企业为了解市民对这四种不同口味粽子的喜爱情况,在端午节前派调查组到各社区调查,第一组抽取了某社区10%的居民调查,并将调查情况绘制成如下两幅不完整的统计图.
(1)这个社区的居民共有多少人?
(2)补全条形统计图.
(3)若该市有20万居民,请估计爱吃C种粽子的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一个角是70°,则其底角为( )
A.70°
B.55°
C.70°或55°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】数据1、2、3、4、5;这组数据的极差是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】四个不相等的整数a,b,c,d,它们的积等于abcd=9,那么a+b+c+d的值是( )
A. 0 B. 4 C. 3 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式从左到右的变形,属于因式分解的是( )
A. a(x﹣y)=ax﹣ayB. x2+3x+2=x(x+3)+2
C. (x+y)(x﹣y)=x2﹣y2D. x3﹣x=x(x+1)(x﹣1)
相关试题

