搜索
【题目】如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为6 m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是
A. AB=12 m B. MN∥AB
C. △CMN∽△CAB D. CM∶MA=1∶2
参考答案：
【答案】D
【解析】
根据三角形中位线的定义和定理及相似三角形的判定定理来分析判断即可.三角形中位线定义：连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半；平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似.
∵M、N分别是 AC、BC 的中点，
∴ MN是△ABC 的中位线，
∴ MN∥AB,故B正确;
∴ MN=
AB,AB=2MN=12m，故A正确；
∴ △CMN∽△CAB，故C正确；
∴CM∶MA=1∶1，故D错误；
所以本题答案应为：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，长方形ABCD中，AB＝6，第1次平移将长方形ABCD沿AB的方向向右平移5个单位，得到长方形A1B1C1D1，第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位，得到长方形A2B2C2D2，…，以此类推，第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向向右平移5个单位，得到长方形AnBnCnDn（n＞2），则ABn长为 （ ）
A. 5n＋6B. 5n＋1C. 5n＋4D. 5n＋3
-
科目： 来源： 题型：
查看答案和解析>>【题目】现有小莉，小罗，小强三个自愿献血者，两人血型为O型，一人血型为A型．若在三人中随意挑选一人献血，两年以后又从此三人中随意挑选一人献血，试求两次所抽血的血型均为O型的概率．（要求：用列表或画树状图的方法解答）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，CE⊥AB于E，BF⊥AC于F，在不添加字母的情况下，找出图中所有的相似三角形，并证明其中一组．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=
BC，连接OE．下列结论：①∠CAD=30°；②SABCD=ABAC；③OB=AB；④OE=
BC，成立的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．
（1）如图①，当直线l与⊙O相切于点C时，求证：AC平分∠DAB；
（2）如图②，当直线l与⊙O相交于点E，F时，求证：∠DAE=∠BAF． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：线段
、
、
；求作：△ABC，使
， 
， 
；
【答案】答案见解析
【解析】试题分析：先画出与
相等的角，再画出
的长，连接
，则
即为所求三角形．试题解析：如图所示：①先画射线BC，
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′；
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧，交于点E；
④在BF上取点C，使CB=a，以B为圆心，c为半径画圆交BE的延长线于点A，连接AC，
结论：△ABC即为所求三角形.
【题型】解答题
【结束】
15【题目】已知：线段
， 
，求作： 
，使
， 
．
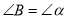相关试题
