【题目】已知正方形![]() 的边长是
的边长是![]() ,
,![]() 是等边三角形,点
是等边三角形,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,则
上,则![]() 的边长是( )
的边长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
根据正方形及等边三角形的性质易证△ABP≌△ADQ,即可得BP=DQ,所以PC=CQ;设BP的长为xcm,则PC=CQ=(10-x)cm,在Rt△ABP中根据勾股定理可得AP=![]() cm;在Rt△PCQ中根据勾股定理可列方程
cm;在Rt△PCQ中根据勾股定理可列方程![]() ,解方程求得x的值,即可求得BP的长.
,解方程求得x的值,即可求得BP的长.
∵正方形ABCD,△APQ是等边三角形,
∴AB=BC=CD=DA,∠B=∠D=90°,AP=AQ=PQ,
∴△ABP≌△ADQ,
∴BP=DQ,
∴PC=CQ,
设BP的长为xcm,则PC=CQ=(10-x)cm,
在Rt△ABP中,AP=![]() cm,
cm,
在Rt△PCQ中,PQ![]() cm,CP=CQ=(10-x)cm,
cm,CP=CQ=(10-x)cm,
∴,![]()
解得:x1=20-10![]() ,x2=20+10
,x2=20+10![]() >10(舍去)
>10(舍去)
∴BP的边长是(20-10![]() )cm.
)cm.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形
 中,
中, ,对角线
,对角线 于
于 点,点
点,点 在
在 轴上,点
轴上,点 、
、 在
在 轴上.
轴上. 若
若 ,
, ,求点
,求点 的坐标;
的坐标; 若
若 ,
, ,求过
,求过 点的反比例函数的解析式;
点的反比例函数的解析式; 如图,在
如图,在 上有一点
上有一点 ,连接
,连接 ,过
,过 作
作 交
交 于
于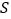 ,交
,交 于
于 ,在
,在 上取
上取 ,过
,过 作
作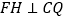 交
交 于
于 ,交
,交 于
于 ,当
,当 在
在 上运动时,(不与
上运动时,(不与 、
、 重合),
重合), 的值是否发生变化?若变化,求出变化范围;若不变,求出其值.
的值是否发生变化?若变化,求出变化范围;若不变,求出其值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列对矩形的判定:“
 对角线相等的四边形是矩形;
对角线相等的四边形是矩形; 对角线互相平分且相等的四边形是矩形;
对角线互相平分且相等的四边形是矩形; 有一个角是直角的四边形是矩形;
有一个角是直角的四边形是矩形; 有四个角是直角的四边形是矩形;
有四个角是直角的四边形是矩形; 四个角都相等的四边形是矩形;
四个角都相等的四边形是矩形; 对角线相等,且有一个直角的四边形是矩形;
对角线相等,且有一个直角的四边形是矩形; 一组邻边垂直,一组对边平行且相等的四边形是矩形;
一组邻边垂直,一组对边平行且相等的四边形是矩形; 对角线相等且互垂直的四边形是矩形”中,正确的个数有( )
对角线相等且互垂直的四边形是矩形”中,正确的个数有( )A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形
 的一组邻边
的一组邻边 、
、 向形外作等边三角形
向形外作等边三角形 、
、 ,则下列结论中错误的是( )
,则下列结论中错误的是( )A.
 平分
平分 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴

解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形
 是菱形,
是菱形, 是正三角形,
是正三角形, 、
、 分别在
分别在 、
、 上,且
上,且 ,则
,则 ____度.
____度.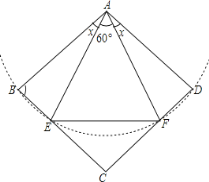
-
科目: 来源: 题型:
查看答案和解析>>【题目】从不同的方向看同一物体时,可能看到不同的图形.其中,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫俯视图.由若干个(大于
 个)大小相同的正方体组成一个几何体的主视图和俯视图如图所示,则这个几何体的左视图不可能是( )
个)大小相同的正方体组成一个几何体的主视图和俯视图如图所示,则这个几何体的左视图不可能是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

