Question

【题目】如图，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．
（1）求证：EB=GD；
（2）判断EB与GD的位置关系，并说明理由；
（3）若AB=2，AG= ，求EB的长．

Answer 1

【答案】
（1）证明：在△GAD和△EAB中，∠GAD=90°+∠EAD，∠EAB=90°+∠EAD

∴∠GAD=∠EAB，

∵四边形EFGA和四边形ABCD是正方形，

∴AG=AE，AB=AD，

在△GAD和△EAB中，

，

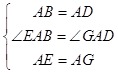∴△GAD≌△EAB（SAS），

∴EB=GD；

（2）解：EB⊥GD．

理由如下：∵四边形ABCD是正方形，

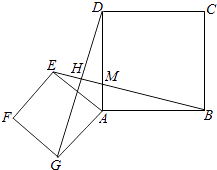
∴∠DAB=90°，

∴∠AMB+∠ABM=90°，

又∵△AEB≌△AGD，

∴∠GDA=∠EBA，

∵∠HMD=∠AMB（对顶角相等），

∴∠HDM+∠DMH=∠AMB+∠ABM=90°，

∴∠DHM=180°﹣（∠HDM+∠DMH）=180°﹣90°=90°，

∴EB⊥GD．

（3）解：连接AC、BD，BD与AC交于点O，

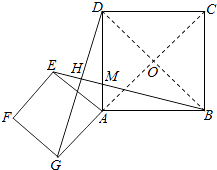
∵四边形ABCD是正方形，

∴BD⊥CG，

∵AB=AD=2，在Rt△ABD中，DB= ，

在Rt△AOB中，OA=OB，AB=2，由勾股定理得：2AO2=22，

OA= ，

即OG=OA+AG= + =2 ，

∴EB=GD= ．

【解析】（1）在△GAD和△EAB中，∠GAD=90°+∠EAD，∠EAB=90°+∠EAD，得到∠GAD=∠EAB从而△GAD≌△EAB，即EB=GD；（2）EB⊥GD，由（1）得∠ADG=∠ABE则在△BDH中，∠DHB=90°所以EB⊥GD；（3）设BD与AC交于点O，由AB=AD=2在Rt△ABD中求得DB，所以得到结果．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．