【题目】如图,直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=AC,过点B作BE⊥AC于点E.

(1)求证:△ADC≌△BEA;
(2)若AD=4,CD=3,求BC的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)首先根据垂直可得∠1=∠D=90°,再根据AB∥CD可得∠2=∠3,然后再有条件AC=BC可利用ASA证明△ADC≌△BEA;
(2)首先根据全等三角形的性质可得AD=BE=4,AE=CD=3,在Rt△ADC中利用勾股定理可得AC=5,然后再在Rt△CEB中利用勾股定理计算出BC长即可.
试题解析:(1)∵BE⊥AC,∴∠1=90°,∵AB∥CD,∴∠2=∠3,在△ADC和△BEA中,∵∠2=∠3,AC=BC,∠1=∠D,∴△ADC≌△BEA(ASA);
(2)∵△ADC≌△BEA,∴AD=BE=4,AE=CD=3,在Rt△ADC中:AC=![]() ,∴CE=5﹣3=2,在Rt△CEB中:BC=
,∴CE=5﹣3=2,在Rt△CEB中:BC=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A.3
B.6
C.8
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年5月23日起,我市将对行人闯红灯分三档进行处罚,九年级数学研究学习小组在某十字路口随机调查部分市民对该法归的了解情况,统计结果后绘制了如图的三副不完整的统计图,请结合图中相关数据回答下列问题.
得分
A
50<n≤60
B
60<n≤70
C
70<n≤80
D
80<n≤90
E
90<n≤100
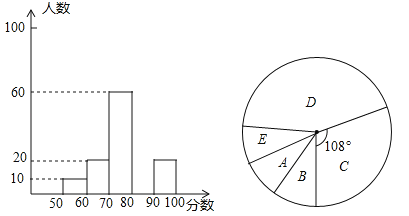
(1)本次共调查的人数为 ;
(2)补全频数分布图;
(3)在扇形统计图中,“B”所在的扇形的圆心角的度数为 ;
(4)若在这一周里,该路口共有2000人通过,则可估计得分在80以上的人数大约为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为丰富学生的校园生活,准备从友谊体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同、每个篮球的价格相同),若购买3个篮球和2个足球共需420元;购买2个篮球和4个足球共需440元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需要从该体育用品商店一次性购买足球和篮球共20个.要求购买篮球数不少于足球数的2倍,总费用不超过1840元,那么这所中学有哪几种购买方案?哪种方案所需费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG =FC;③AG∥FC;④S△FGC =
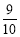 .其中正确的是( )
.其中正确的是( )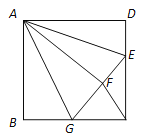
A.①② B.②④ C.①②③ D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若样本1,2,3,x的平均数为5,又知样本1,2,3,x,y的平均数为6,那么样本1,2,3,x,y的方差是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC与△DEF相似且面积比为9∶25,则△ABC与△DEF的相似比为____.
相关试题

