【题目】如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,过A作AG∥DE交射线EB于点G,点F恰好是AD中点。
(1)求证:△AFG≌△DFE;
(2)若BC=CE,①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
参考答案:
【答案】
(1)证明:∵AG∥DE,∴∠G=∠DEF,
∵△AGF和△DEF中,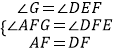 ,
,
∴△AGF≌△DEF(AAS)
(2)解:①证明:∵BC=CE,∴∠CBE=∠CEB,
∵∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,
∴∠ABF=∠DEF;
②∵△AGF≌△DEF,
∴∠G=∠DEF,
∵∠ABF=∠DEF,
∴∠ABF=∠G,
∴AG=AB,
∵△AGF≌△DEF,
∴AG=DE,
∴DE=AB,
∵△ABC和△DEC中,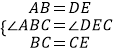 ,
,
∴△ABC≌△DEC(SAS)
∴AC=CD,∠BAC=∠EDC,
∵AC∥DE,
∴∠EDC=∠ACD,
∴∠ACD=∠BAC=30°,
∴∠CAD=75°,
∵∠ABF=∠G,∠BAC=30°,
∴∠G=15°,
∵∠CAD=∠G+∠AFG,
∴∠AFG=60°
【解析】(1)由平行线的性质得到内错角相等,根据全等三角形的判定方法AAS,得到△AGF≌△DEF;(2)由角的和差得到∠ABF=∠DEF;由(1)得到全等三角形的对应边、对应角相等,根据SAS,得到△ABC≌△DEC,得到对应边、对应角相等,由角的和差求出∠AFG的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
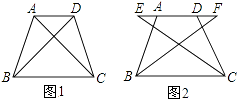
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )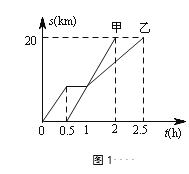
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个数中,是负数的是( )
A. |﹣2|B. (﹣2)2C. ﹣(﹣2)D. ﹣|﹣2|
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE 是⊙O的切线,连结OD,OE
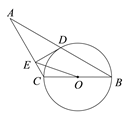
(1)求证:∠DEA=90°;
(2)若BC=4,写出求 △OEC的面积的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蓄水池的横断面示意图如右图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度
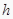 和放水时间
和放水时间 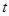 之间的关系的是( )
之间的关系的是( )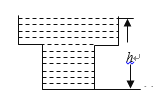
A.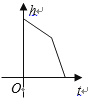
B.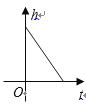
C.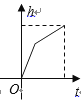
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
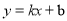 与x轴交于点A(1,0),与 y交于点B(0,-2).
与x轴交于点A(1,0),与 y交于点B(0,-2).(1)求直线AB的表达式;
(2)点C是直线AB上的点,且CA=AB,过动点P(m,0)且垂直于x轴的直线与直线AB 交于点D,若点D不在线段BC上,写出m的取值范围.
相关试题

