【题目】对某一个函数给出如下定义:如果存在实数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ,那么称这个函数是有上界函数,在所有满足条件的
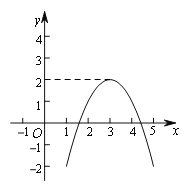
,那么称这个函数是有上界函数,在所有满足条件的![]() 中,其最小值称为这个函数的上确界.例如下图中的函数是有上界函数,其上确界是2.
中,其最小值称为这个函数的上确界.例如下图中的函数是有上界函数,其上确界是2.
(1)分别判断函数![]() (
(![]() )和
)和![]() (
(![]() )是不是有上界函数?如果是有上界函数,求其上确界;
)是不是有上界函数?如果是有上界函数,求其上确界;
(2)如果函数![]() (
(![]() )的上确界是
)的上确界是![]() ,且这个函数的最小值不超过
,且这个函数的最小值不超过![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若函数![]() (
(![]() )是以3为上确界的有上界函数,求
)是以3为上确界的有上界函数,求![]() 值.
值.
参考答案:
【答案】(1)y=![]() (x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;(2)-1≤a<1;(3)
(x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;(2)-1≤a<1;(3)![]() .
.
【解析】
试题分析:(1)根据有界函数函数的定义和上确界定义分析即可;
(2)根据函数的上确界和函数增减性得到2-a=b,函数的最小值为2-b,根据b>a,函数的最小值不超过2a+1,列不等式求解集即可;
(3)根据对称轴方程x=a和上确界为3,分类讨论a≤3时和a>3时,列方程求解.
试题解析:(1)根据有界函数定义,y=![]() (x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;
(x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;
(2)∵在y=-x+2中,y随x的增大而减小,
∴上确界为2-a,即2-a=b,
又b>a,所以2-a>a,解得a<1,
∵函数的最小值是2-b,∴2-b≤2a+1,得a≤2a+1,解得a≥-1,
综上所述:-1≤a<1;
(3)函数的对称轴为x=a,
①当a≤3时,函数的上确界是25-10a+2=27-10a,
∴27-10a=3,解得a=![]() ,符合题意;
,符合题意;
②当a>3时,函数的上确界是1-2a+2=3-2a,
∴3-2a=3,解得a=0,不符合题意.
综上所述:a=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各线段的长度成比例的是( )
A. 2 cm,5 cm,6 cm,8 cm B. 1 cm,2 cm,3 cm,4 cm
C. 3 cm,6 cm,7 cm,9 cm D. 3 cm,6 cm,9 cm,18 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组图形中,一定相似的是( )
A. 正方形与矩形 B. 正方形与菱形
C. 菱形与菱形 D. 正五边形与正五边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a是偶数时,(x﹣y)a(y﹣x)b与(y﹣x)a+b的关系是( )
A.相等
B.互为倒数
C.互为相反数
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使
 ,那么平行四边形ABCD应满足的条件是【 】
,那么平行四边形ABCD应满足的条件是【 】
A.∠ABC=60° B.AB:BC=1:4 C.AB:BC=5:2 D.AB:BC=5:8
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年“3.15”期间某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:同一日内,顾客在本商场每消费满200元,就可以在箱子里一次摸出两个球,商场根据两小球所标金额之和返还相应数额的购物券.某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请用树状图或列表求出该顾客所获得的购物券金额不低于30元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于两个数,M=2008×20092009,N=2009×20082008.则( )
A. M=N B. M>N C. M<N D. 无法确定
相关试题

