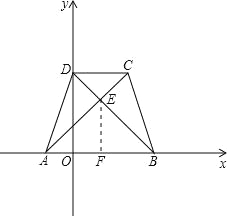
【题目】在平面直角坐标系中,已知等腰梯形ABCD的三个顶点A(-2,0),B(6,0),C(4,6),对角线AC与BD相交于点E.
(1)求E的坐标;
(2)若M是x轴上一动点,求MC+MD的最小值;
(3)在y轴正半轴上求点P,使以P、B、C为顶点的三角形为等腰三角形.

参考答案:
【答案】(1) 点E的坐标为(2,4);(2) ![]() ;(3) 点P的坐标为:(0,6+
;(3) 点P的坐标为:(0,6+![]() ),(0,6-
),(0,6-![]() ),(0,2),(0,
),(0,2),(0,![]() ).
).
【解析】
试题分析:(1)作EF⊥AB,根据已知,可得出OD=6,FB=4,OF=2,然后,根据相似,即可求出EF的长,即可得出点E的坐标;
(2)作点D关于x轴的对称点D′,则D′的坐标为(0,-6),根据两点间的距离公式,算出即可;
(3)设点P(0,y),y>0,分三种情况,①PC=BC;②PB=BC;③PB=PC;解答出即可;
试题解析:(1)作EF⊥AB,
∴![]() ,
,
∵梯形ABCD是等腰梯形,
∴AE=BE,
∴在等腰三角形ABE中,AF=BF,
∵A(-2,0),B(6,0),C(4,6),
∴点D的坐标为(0,6),
∴OD=6,FB=4,OF=2,
∴![]() ,
,
∴EF=4,
∴点E的坐标为(2,4);
(2)由题意可得,
点D关于x轴的对称点D′的坐标为(0,-6),
CD′与x轴的交点为M,
∴此时,MC+MD=CD′为最小值,
∴CD′=![]() ;
;
(3)设点P(0,y),y>0,
分三种情况,①PC=BC;
∴42+(6-y)2=22+62,
解得,y=6±![]() ;
;
②PB=BC;
∴62+y2=22+62,
解得,y=2,y=-2(舍去);
③PB=PC;
∴62+y2=42+(6-y)2,
解得,y=![]() ;
;
综上,点P的坐标为:(0,6+![]() ),(0,6-
),(0,6-![]() ),(0,2),(0,
),(0,2),(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知□ABCD的对角线AC、BD交于O,且∠1=∠2.
(1)求证:□ABCD是菱形;
(2)F为AD上一点,连结BF交AC于E,且AE=AF.求证:AO=
 (AF+AB).
(AF+AB).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元.设2,3月份利润的月增长率为x,那么x满足的方程为( )
A. 10(1+x)2=36.4 B. 10+10(1+x)2=36.4
C. 10+10(1+x)+10(1+2x)=36.4 D. 10+10(1+x)+10(1+x)2=36.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式a2﹣9a的结果是_______________
-
科目: 来源: 题型:
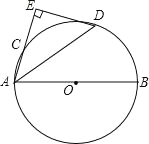
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求AC长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=2x2先向左平移3个单位,再向上平移4个单位,所得抛物线的函数表达式为( )
A. y=2(x+3)2+4 B. y=2(x+3)2﹣4 C. y=2(x﹣3)2﹣4 D. y=2(x﹣3)2+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)某同学在计算多项式M加上x2 -3x+7时,因误认为是加上x2+3x+7,结果得到答案是15x2+2x-4.试问:
(1)M是怎样的整式?
(2)这个问题的正确结果应是多少?
相关试题

