【题目】在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为 . 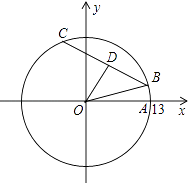
参考答案:
【答案】24
【解析】解:∵直线y=kx﹣3k+4=k(x﹣3)+4,
∴k(x﹣3)=y﹣4,
∵k有无数个值,
∴x﹣3=0,y﹣4=0,解得x=3,y=4,
∴直线必过点D(3,4),
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD=5,
∵以原点O为圆心的圆过点A(13,0),
∴圆的半径为13,
∴OB=13,
∴BD=12,
∴BC的长的最小值为24;
故答案为:24.
根据直线y=kx﹣3k+4必过点D(3,4),求出最短的弦CB是过点D且与该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心的圆过点A(13,0),求出OB的长,再利用勾股定理求出BD,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的周长为20,其中AB=8,
(1)用直尺和圆规作 AB 的垂直平分线 DE 交 AC 于点 E,垂足为 D,连接 EB;(保留作图痕迹,不要求写画法)
(2)在(1)作出 AB 的垂直平分线 DE 后,求△CBE 的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年“五一节”前,某商场用60万元购进某种商品,该商品有甲、乙两种包装共500件,其中每件甲包装中有75个A种产品,每个A产品的成本为12元;每件乙包装中有100个B产品,每个B种产品的成本为14元.商场将A产品标价定为每个18元,B产品标价定为每个20元.
(1)甲、乙两种包装的产品各有多少件?
(2)“五一节”商场促销,将A产品按原定标价打9折销售,B种产品按原定标价打8.5折销售,“五一节”期间该产品全部卖完,该商场销售该商品共获利多少元?
-
科目: 来源: 题型:
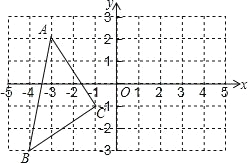
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出与△ABC 关于 y 轴对称的△A1B1C1(要求点 A 与 A1,点 B 与点B1,点 C 和点 C1 相对应);写出点 A1,B1,C1 的坐标(直接写答案)
(2)请求出△A1B1C1 的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( )

A. 3个球 B. 4个球
C. 5个球 D. 6个球
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民出行,减轻城市中心交通压力,某市正在修建贯穿全城南北、东西的地铁1,2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元,且1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线、2号线每千米的平均造价分别是多少亿元;
(2)除1,2号线外,该市规划到2019年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到
 的位置,
的位置, ,
, ,平移距离为6,则阴影部分面积为
,平移距离为6,则阴影部分面积为


A. 24 B. 40 C. 42 D. 48
相关试题

