Question

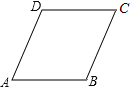
【题目】如图，凸四边形ABCD中，AB∥CD，且AB+BC=CD+AD．求证：ABCD是平行四边形。

Answer 1

【答案】详见解析.

证明：假设ABCD不是平行四边形，即AB≠CD，

不妨设AB＞CD．在AB边上取点E，使AE=CD，则AECD是平行四边形，

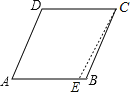
∴AD=CE，

由AB+BC=CD+AD，

即（AE+EB）+BC=CD+AD，

∴EB+BC=CE，与三角形不等式EB+BC＞CE矛盾，

因此，ABCD必是平行四边形。

【解析】试题分析：

利用已知条件不能直接证明四边形ABCD是平行四边形，故考虑用反证法，假设四边形ABCD不是平行四边形，则可设AB＞CD，所以在AB上取点E，使AE=CD，然后经过推理得出矛盾，从而假设不成立，故原命题成立.

试题解析：

证明：假设ABCD不是平行四边形，即AB≠CD，

不妨设AB＞CD．在AB边上取点E，使AE=CD，则AECD是平行四边形，

∴AD=CE，

由AB+BC=CD+AD，

即（AE+EB）+BC=CD+AD，

∴EB+BC=CE，与三角形不等式EB+BC＞CE矛盾，

因此，ABCD必是平行四边形。