【题目】已知梯形ABCD,请使用无刻度直尺画图.
(1)在图1中画出一个与梯形ABCD面积相等,且以CD为边的三角形;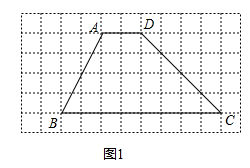
(2)图2中画一个与梯形ABCD面积相等,且以AB为边的平行四边形.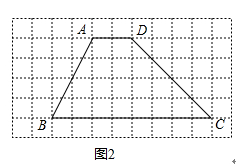
参考答案:
【答案】
(1)
解:设小正方形的边长为1,则S梯形ABCD= ![]() (AD+BC)×4=
(AD+BC)×4= ![]() ×10×4=20,
×10×4=20,
∵CD=4 ![]() ,
,
∴三角形的高=20×2÷4 ![]() =5
=5 ![]() ,如图1,△CDE就是所作的三角形,
,如图1,△CDE就是所作的三角形,
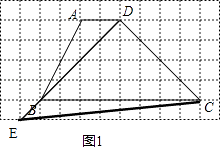
(2)
如图2,BE=5,BE边上的高为4,
∴平行四边形ABEF的面积是5×4=20,
∴平行四边形ABEF就是所作的平行四边形.
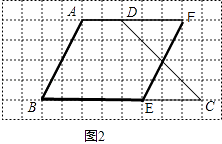
【解析】(1)求出三角形CD边上的高作图,(2)找出BE及它的高相乘得20,以AB为一边作平行四边形..
【考点精析】根据题目的已知条件,利用三角形的“三线”的相关知识可以得到问题的答案,需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内.
-
科目: 来源: 题型:
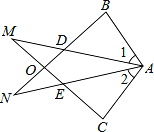
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
-
科目: 来源: 题型:
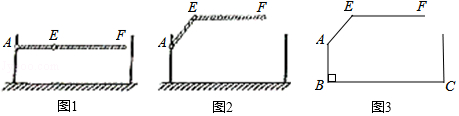
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
-
科目: 来源: 题型:
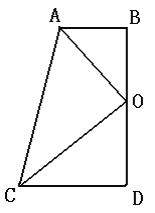
查看答案和解析>>【题目】如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成
 已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.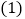 求甲、乙两工程队每天能完成道路的长度分别是多少m?
求甲、乙两工程队每天能完成道路的长度分别是多少m?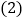 若村委每天需付给甲队的道路改造费用为
若村委每天需付给甲队的道路改造费用为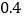 万元,乙队为
万元,乙队为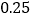 万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点M为直线AB上一动点,
 都是等边三角形,连接BN
都是等边三角形,连接BN  求证:
求证:  ;
; 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系 不需证明
不需证明 ;
; 如图4,当
如图4,当 时,证明:
时,证明:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:
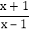 =
= =
=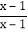 +
+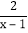 =1+
=1+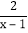 ,
,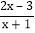 =
=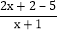 =
=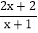 +
+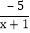 =2+
=2+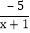 ,则
,则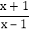 和
和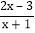 都是“和谐分式”.
都是“和谐分式”.(1)下列分式中,属于“和谐分式”的是______(填序号);
①
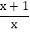 ;②
;②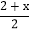 ;③
;③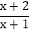 ;④
;④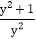
(2)将“和谐分式”
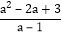 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为: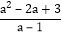 =______+______;
=______+______;(3)应用:先化简
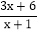 -
-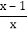 ÷
÷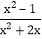 ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
相关试题

