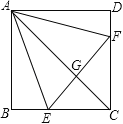
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个

A. 4 B. 3 C. 2 D. 1
参考答案:
【答案】C
【解析】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
![]() ,
,
Rt△ABE≌Rt△ADF(HL),
∴BE=DF(故①正确).
∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°(故②正确),
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF.(故③正确).
设EC=x,由勾股定理,得
EF=x,CG=![]() x,
x,
AG=AEsin60°=EFsin60°=2×CGsin60°=![]() x,
x,
∴AC=![]() ,
,
∴AB=![]() ,
,
∴BE=![]() ﹣x=
﹣x=![]() ,
,
∴BE+DF=x﹣x≠x,(故④错误),
∵S△CEF=![]() ,
,
S△ABE=![]() =
=![]() ,
,
∴2S△ABE=![]() =S△CEF,(故⑤正确).
=S△CEF,(故⑤正确).
综上所述,正确的有4个,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为
 (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为 (元),图中折线OAB表示
(元),图中折线OAB表示 与x之间的函数关系.
与x之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求
 、
、 与x的函数表达式;
与x的函数表达式;(3)在图中画出
 与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
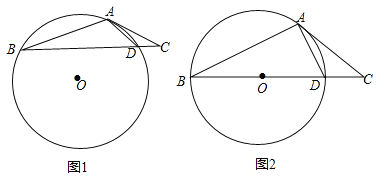
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形纸片的一边AD,使点D落在BC边上的点F处,已知BC=10cm,AB=8cm,求EC的长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的是( )
A. 若a是实数,则|a|≥0 B. 抛一枚硬币,正面朝上
C. 明天会下雨 D. 打开电视,正在播放新闻
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程x2﹣x=0的两根为x1,x2(x1<x2),则x2﹣x1=______.
相关试题

