Question

【题目】如图所示，△ABC中，A（﹣2，1）、B（﹣4，﹣2）、C（﹣1，﹣3），△A′B′C′是△ABC平移之后得到的图，并且C的对应点C′的坐标为（4，1）。

（1）A′、B′.两点的坐标分别为A′　　　　　　、B′　　　　　　；

（2）请作出△ABC平移之后的图形△A′B′C′；

（3）求△A′B′C′的面积．

Answer 1

【答案】（1）（3,5），（1,2）；（2）见解析；（3）.

【解析】

（1）由点C（﹣1，﹣3）平移到C′（4，1）可知，图形的平移规律是：先向右平移5个单位，再向上平移4个单位，根据此规律即可求出A′、B′的坐标；

（2）描出A′、B′、C′三点的坐标，再依次连接即可；

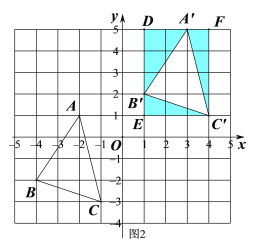
（3）如图2，S△A'B'C'= S矩形C'EDF－S△A'C'F－S△A'B'D－S△B'C'E，再代入数据进行计算即可.

解：（1）由点C（﹣1，﹣3）平移到C′（4，1）可知，图形的平移规律是：先向右平移5个单位，再向上平移4个单位，所以A′、B′的坐标分别是（﹣2+5，1+4）、（﹣4+5，﹣2+4），即A′（3，5）、B′（1，2）；

故答案为（3，5），（1，2）；

（2）如图1，△A′B′C′即为所求.

（3）如图2，S△A'B'C'= S矩形C'EDF－S△A'C'F－S△A'B'D－S△B'C'E

=

=.