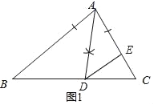
【题目】如图所示,在△ABC中,已知线段AD平分∠BAC交BC于D,∠B=62°,∠C=58°.
(1)用尺规作出线段AD,并求∠ADB的度数;
(2)若DE⊥AC于点E,把图形补充完整并求∠ADE的度数.

参考答案:
【答案】(1)88°;(2)60°.
【解析】
(1)根据角平分线的作图方法得到AD,再根据三角形的内角和即可求解;
(2)作DE⊥AC于点E,根据∠ADE与∠CAD互余即可得解.
解:(1)∵在△ABC中,∠B=62°,∠C=58°,∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣∠B﹣∠C=60°.
∵AD是△ABC的角平分线,
∴∠BAD=![]() ∠BAC=30°,
∠BAC=30°,
在△ABD中,∠B=62°,∠BAD=30°,
∴∠ADB=180°﹣∠B﹣∠BAD=88°;
(2)作DE⊥AC于点E,
∵∠CAD=![]() ∠BAC=30°,
∠BAC=30°,
又∵DE⊥AC,
∴在Rt△ADE中,∠EAD=30°,
∴∠ADE=90°﹣∠EAD=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,请仔细观察并找出规律,解答下列问题:

(1)按照此规律,摆第n个图时,需用火柴棒的根数是多少?
(2)求摆第50个图时所需用的火柴棒的根数;
(3)按此规律用1202根火柴棒摆出第n个图形,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E.
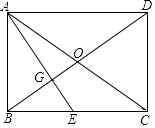
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.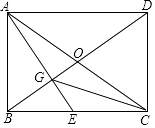
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个分别含有30°,45°角的一副直角三角板.
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知数轴上点A表示的数为8,B是数轴上一点,且AB=22.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数____,点P表示的数____(用含t的代数式表示);
(2)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(列一元一次方程解应用题)
(3)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问 秒时P、Q之间的距离恰好等于2(直接写出答案)
(4)思考在点P的运动过程中,若M为AP的中点,N为PB的中点.线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.

-
科目: 来源: 题型:
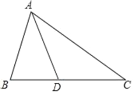
查看答案和解析>>【题目】如图,在△ABC中,点D在AC的垂直平分线上.
(1)若AB=AD,∠BAD=26°,求∠B和∠C的度数;
(2)若AB=AD=DC,AC=BC,求∠C的度数;
(3)若AC=6,△ABD的周长为13cm,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:销售单价(元)
x
销售量y(件)
销售玩具获得利润w(元)
(2)在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具车规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌服装获得的最大利润是多少?
相关试题

