【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_____.

参考答案:
【答案】3或6.
【解析】
当![]() 为直角三角形时,有两种情况:
为直角三角形时,有两种情况:
①当点![]() 落在矩形内部时,如答图1所示.
落在矩形内部时,如答图1所示.
连结![]() ,先利用勾股定理计算出
,先利用勾股定理计算出![]() ,根据折叠的性质得
,根据折叠的性质得![]() ,而当
,而当![]() 为直角三角形时,只能得到
为直角三角形时,只能得到![]() ,所以点
,所以点![]() 、
、![]() 、
、![]() 共线,即
共线,即![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,则
处,则![]() ,
,![]() ,可计算出
,可计算出![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,然后在
,然后在![]() 中运用勾股定理可计算出
中运用勾股定理可计算出![]() .
.
②当点![]() 落在
落在![]() 边上时,如答图2所示.此时四边形
边上时,如答图2所示.此时四边形![]() 为正方形.
为正方形.
解:当![]() 为直角三角形时,有两种情况:
为直角三角形时,有两种情况:
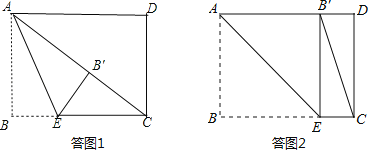
①当点![]() 落在矩形内部时,如答图1所示.
落在矩形内部时,如答图1所示.
连结![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,
处,
![]() ,
,
当![]() 为直角三角形时,只能得到
为直角三角形时,只能得到![]() ,
,
![]() 点
点![]() 、
、![]() 、
、![]() 共线,即
共线,即![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,如图,
处,如图,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ;
;
②当点![]() 落在
落在![]() 边上时,如答图2所示.
边上时,如答图2所示.
此时![]() 为正方形,
为正方形,
![]() .
.
综上所述,![]() 的长为3或6.
的长为3或6.
故答案为:3或6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= BC,成立的个数有( )
BC,成立的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下数表是由1开始的连续自然数组成的,观察规律并完成各题的解答.

(1)表示第9行的最后一个数是 .
(2)用含n的代数式表示:第n行的第一个数是 ,第n行共有 个数;第n行各数之和是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
相关试题

