【题目】
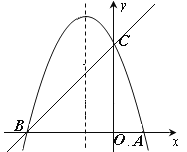
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
⑴若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
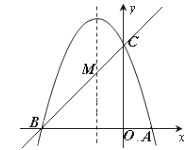
⑵在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标;⑶设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)M(-1,2);(3)满足条件的点P共有四个,分别为
;(2)M(-1,2);(3)满足条件的点P共有四个,分别为![]() (-1,-2),
(-1,-2), ![]() (-1,4),
(-1,4), ![]() (-1,
(-1,![]() ) ,
) ,![]() (-1,
(-1,![]() ).
).
【解析】
试题分析:(1)已知抛物线y=ax2+bx+c的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,可得方程组,解方程组可求得a、b、c的值,即可得抛物线的解析式;根据抛物线的对称性和点A的坐标(1,0)可求得B点的坐标(-3,0),用待定系数法可求得直线BC的解析式;(2)使MA+MC最小的点M应为直线BC与对称轴x=-1的交点,把x=-1代入直线BC的解析式求得y的值,即可得点M的坐标;(3)分①B为直角顶点,②C为直角顶点,③P为直角顶点三种情况分别求点P的坐标.
试题解析:(1)依题意,得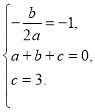 解之,得
解之,得
∴抛物线解析式为![]() .
.
∵对称轴为x=-1,且抛物线经过A(1,0),
∴B(-3,0).
把B(-3,0)、C(0,3)分别直线y=mx+n,得
![]() 解之,得
解之,得![]()
∴直线BC的解析式为![]() .
.
(2)∵MA=MB,∴MA+MC=MB+MC.
∴使MA+MC最小的点M应为直线BC与对称轴x=-1的交点.
设直线BC与对称轴x=-1的交点为M,把x=-1
代入直线![]() ,得y=2.
,得y=2.
∴M(-1,2)
(3)设P(-1,t),结合B(-3,0),C(0, 3),得BC2=18,
PB2=(-1+3)2+t2=4+t2,
PC2=(-1)2+(t-3)2=t2-6t+10.
①若B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10.
解之,得t=-2.
②若C为直角顶点,则BC2+PC2=PB2,即
18+t2-6t+10=4+t2.解之,得t=4.
③若P为直角顶点,则PB2+PC2=BC2,即
4+t2+t2-6t+10=18.解之,得t1=![]() ,t2=
,t2=![]() .
.
综上所述,满足条件的点P共有四个,分别为![]() (-1,-2),
(-1,-2), ![]() (-1,4),
(-1,4), ![]() (-1,
(-1,![]() ) ,
) ,![]() (-1,
(-1,![]() ).
).
-
科目: 来源: 题型:
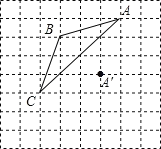
查看答案和解析>>【题目】如图,正方形网格中每个小正方形的边长为1,格点△ABC的顶点A(1,2)、B(﹣2,1), 将△ABC平移得到△A′B′C′,使得点A的对应点A′,试解答下列问题:
(1)根据题意,在网格中建立平面直角坐标系;
(2)画出△A′B′C′,并写出点C′的坐标为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=-2,a-b=4,则a2-b2=
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断不正确的是( )
A.四个角相等的四边形是矩形B.对角线垂直的四边形是菱形
C.对角线相等的平行四边形是矩形D.对角线垂直的平行四边形是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式:①﹣(﹣2);②﹣|﹣2|;③﹣22;④﹣(﹣2)2 , 计算结果为负数的个数有( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】算24点游戏是一种使用扑克牌来进行的益智类游戏,游戏内容是:从一副扑克牌中抽去大小王剩下52张,任意抽取4张牌,把牌面上的数运用你所学过的加、减、乘、除、乘方运算得出24.每张牌都必须使用一次,但不能重复使用.
(1)如图1,在玩“24点”游戏时,小明抽到以下4张牌:

请你帮他写出运算结果为24的算式:(写出2个); 、 ;
(2)如图2,如果
 、
、 表示正,
表示正, .
. 表示负,J表示11点,Q表示12点.请你用下列4张牌表示的数写出运算结果为24的算式(写出1个): .
表示负,J表示11点,Q表示12点.请你用下列4张牌表示的数写出运算结果为24的算式(写出1个): . -
科目: 来源: 题型:
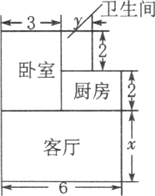
查看答案和解析>>【题目】小王购买了一套经济适用房,他准备在地面铺上地砖,地面结构如图所示,根据图中的数据(单位:米),解答下面的问题:
(1)用含x、y的整式表示地面的总面积;
(2)如果每平方米地砖的价格为200元,那么铺地砖的总费用为多少元?
相关试题

