【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求二次函数的表达式;
(2)设上述抛物线的对称轴![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,
, ![]() 为线段
为线段![]()
上一点, ![]() 为
为![]() 轴负半轴上一点,以
轴负半轴上一点,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似;
相似;
满足条件的![]() 点有且只有一个时,求
点有且只有一个时,求![]() 的取值范围;
的取值范围;
②若满足条件的![]() 点有且只有两个,直接写出
点有且只有两个,直接写出![]() 的值.
的值.
参考答案:
【答案】(2)![]() ;(2)①
;(2)①![]() ;②1或
;②1或![]()
【解析】试题分析:(1)设抛物线的解析式为y=a(x+1)(x-3),将C(0,3)代入求得a的值可得到抛物线的解析式;
(2)先求得点C的坐标,从而得到ED的长,然后再求得抛物线的对称轴,从而得到CE的长,然后设PE=x,则PD=3-x,然后分为△CEP∽△QDP和△CEP∽△PDQ两种情况列出比例式,从而得到m与x的函数关系,然后依据函数关系可确定出m的取值范围,①依据符合条件的点P只有一个,然后找出仅能够使得其中一个三角形的相似时,m的范围即可;②找出能够使得两种情况都成立时,m的范围即可.
试题解析:(1)设抛物线的解析式为y=a(x+1)(x-3),
将C(0,3)代入得:3=-3a,解得a=-1,
∴抛物线的解析式为y=-x2+2x+3.
(2)∵x=-![]() =1,
=1,
∴CE=1.
将x=0代入抛物线的解析式得:y=3,
∴点C(0,3).
∴ED=3.
设EP=x,则(0<x<3).
当△CEP∽△QDP时,则![]() ,即
,即![]() ,
,
整理得:m=2-![]() ,
,
∴m随x的增大而增大,
∴m<1.
∵Q在x轴的负半轴上,
∴m<0.
当△CEP∽△PDQ时, ![]() ,即
,即![]() ,整理得:m=x2-3x+1,
,整理得:m=x2-3x+1,
∴当x=![]() 时,m有最小值,m的最小值=-
时,m有最小值,m的最小值=-![]() .
.
又∵Q在x轴的负半轴上,
∴m<0.
∴-![]() ≤m<0.
≤m<0.
①∵当m<-![]() 时,有且只有△CEP∽△QDP一种情况,
时,有且只有△CEP∽△QDP一种情况,
∴当m<-![]() 时,满足条件的点P有且只有一个.
时,满足条件的点P有且只有一个.
②当-![]() ≤m<0时,存在△CEP∽△QDP或△CEP∽△PDQ两种情况,
≤m<0时,存在△CEP∽△QDP或△CEP∽△PDQ两种情况,
∴当-![]() ≤m<0时,满足条件的P点有且只有两个.
≤m<0时,满足条件的P点有且只有两个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,则a2-b2+6b的值为( )
A. 6B. 9C. 12D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查发现:在一段时间内,当销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.若商场要获得10000元销售利润,该玩具销售单价应定为多少元?售出玩具多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在国际跳水比赛中,根据规则,需要有7位裁判对选手的表现进行打分.在裁判完成打分后,总裁判会在7位裁判的打分中,去掉一个最高分,再去掉一个最低分,将剩下5位裁判的平均分作为该选手的最终得分.在总裁判去掉最高分与最低分后,一定保持不变的统计量是( )
A. 平均分B. 众数C. 中位数D. 最高分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果把高于警戒水位0.1米,记作+0.1米,则低于警戒水位0.2米,记作( )
A. +0.2米B. -0.2米C. 0.3米D. -0.3米
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,
 是⊙
是⊙ 的直径,
的直径, 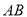 为⊙
为⊙ 的弦,过点
的弦,过点 作
作 ⊥
⊥ ,交
,交 的延长线于点
的延长线于点 .点
.点 在
在 上,且
上,且 .
.
(1)求证:直线
 是⊙
是⊙ 的切线;
的切线;(2)若
 ,
,  ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】连结三角形___________的线段叫做三角形的中位线.
相关试题

