【题目】政府为开发“江心岛O”,从仓储D处调集物资,计划先用汽车运到与D在同一直线上的C,B,A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时, 
(1)求B、C两个码头之间的距离;
(2)这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).
参考答案:
【答案】
(1)解:∵∠OCA=∠D+∠COD,
∴∠COD=30°﹣15°=15°,
∴CO=CD=20,
在Rt△OCA中,∵∠OCA=30°,
∴OA= ![]() OC=10,CA=
OC=10,CA= ![]() OA=10
OA=10 ![]() ≈17,
≈17,
在Rt△OBA中,∵∠OBA=45°,
∴BA=OA=10,OB= ![]() OA≈14,
OA≈14,
∴BC=17﹣10=7
(2)解:当这批物资在C码头装船,运抵小岛O时,所用时间= ![]() +
+ ![]() =1.2(小时);
=1.2(小时);
当这批物资在B码头装船,运抵小岛O时,所用时间= ![]() +
+ ![]() =1.1(小时);
=1.1(小时);
当这批物资在A码头装船,运抵小岛O时,所用时间= ![]() +
+ ![]() =1.14(小时);
=1.14(小时);
所以这批物资在B码头装船,最早运抵小岛O
【解析】(1)利用三角形外角性质计算出∠COD=15°,则CO=CD=20,在Rt△OCA中利用含30度的直角三角形三边的关系计算出OA= ![]() OC=10,CA=
OC=10,CA= ![]() OA≈17,在Rt△OBA中利用等腰直角三角形的性质计算出BA=OA=10,OB=
OA≈17,在Rt△OBA中利用等腰直角三角形的性质计算出BA=OA=10,OB= ![]() OA≈14,则BC=7;(2)根据速度公式分别计算出在三个码头装船,运抵小岛所需的时间,再比较时间的大小进行判断.
OA≈14,则BC=7;(2)根据速度公式分别计算出在三个码头装船,运抵小岛所需的时间,再比较时间的大小进行判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M,N,再分别以点M,N为圆心,大于
 MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=________.
MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=________.
-
科目: 来源: 题型:
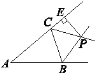
查看答案和解析>>【题目】如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC=2,则S△ABC=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图21所示,海岛上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸的距离相等吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC

(1)求证:BC平分∠PBD;
(2)求证:PC2=PAPB;
(3)若PA=2,PC=2 ,求阴影部分的面积(结果保留π)
,求阴影部分的面积(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】骑自相车旅行越来越受到人们的喜爱,顺风车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%. A、B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
(1)求今年4月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
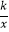 的图象经过点A(﹣
的图象经过点A(﹣ 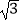 ,1).
,1).
(1)试确定此反比例函数的解析式;
(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;
(3)已知点P(m,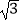 m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是
m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是  ,设Q点的纵坐标为n,求n2﹣2
,设Q点的纵坐标为n,求n2﹣2 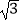 n+9的值.
n+9的值.
相关试题

