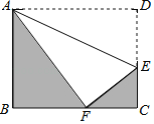
【题目】如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知AD=10cm,BF=6cm.
(1)求DE的值;
(2)求图中阴影部分的面积.
参考答案:
【答案】(1)5;(2)30.
【解析】
(1)由矩形的性质得BC=AD=10,CF=BC﹣BF=4,由折叠的性质得AF=AD=10,在Rt△ABF中,由勾股定理得AB=![]() =8,设EC=x,则DE=EF=8﹣x,在Rt△ECF中,由勾股定理得x2+42=(8﹣x)2,解得x=3,即可得出结果;
=8,设EC=x,则DE=EF=8﹣x,在Rt△ECF中,由勾股定理得x2+42=(8﹣x)2,解得x=3,即可得出结果;
(2)由S阴影=S△ABF+S△CEF,即可得出结果.
解:(1)∵四边形ABCD是矩形,
∴BC=AD=10,CF=BC﹣BF=10﹣6=4,
由折叠的性质得AF=AD=10,
在Rt△ABF中,由勾股定理得:AB=8,
设EC=x,则DE=EF=8﹣x,
在Rt△ECF中,由勾股定理得:x2+42=(8﹣x)2,
解得:x=3,
∴EC=3,DE=8﹣3=5(cm);
(2)S阴影=S△ABF+S△CEF=![]() ×6×8+
×6×8+![]() ×4×3=30(cm2).
×4×3=30(cm2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣
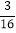 x2+bx+c的图象经过A(0,3),B(﹣4,﹣
x2+bx+c的图象经过A(0,3),B(﹣4,﹣ )两点.
)两点.(1)求b,c的值.
(2)二次函数y=﹣
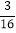 x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】某驻村扶贫小组为解决当地贫困问题,带领大家致富.经过调查研究,他们决定利用当地生产的甲乙两种原料开发A,B两种商品,为科学决策,他们试生产A、B两种商品100千克进行深入研究,已知现有甲种原料293千克,乙种原料314千克,生产1千克A商品,1千克B商品所需要的甲、乙两种原料及生产成本如下表所示.
甲种原料(单位:千克)
乙种原料(单位:千克)
生产成本(单位:元)
A商品
3
2
120
B商品
2.5
3.5
200
设生产A种商品x千克,生产A、B两种商品共100千克的总成本为y元,根据上述信息,解答下列问题:
(1)求y与x的函数解析式(也称关系式),并直接写出x的取值范围;
(2)x取何值时,总成本y最小?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.

(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.

⑴写出A′、B′、C′的坐标;
⑵求出△ABC的面积;
⑶点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=ax﹣a与y=
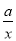 (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )A.
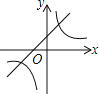 B.
B.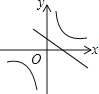
C.
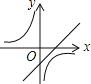 D.
D.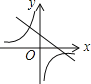
-
科目: 来源: 题型:
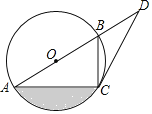
查看答案和解析>>【题目】如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
相关试题

