【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

参考答案:
【答案】![]() ;
;![]() 点
点![]() 或
或![]() ;
;![]() 点P的坐标为
点P的坐标为![]() 或
或![]() .
.
【解析】
(1)由B、C坐标,根据待定系数法可求得直线AB的解析式;(2)由(1)列出AB的方程,求出B的坐标,求出![]() 的面积和
的面积和![]() 的面积,设P的纵坐标为m,代值求出m,再列出直线OC的解析式为
的面积,设P的纵坐标为m,代值求出m,再列出直线OC的解析式为![]() ,当点P在OC上时,求出P点坐标,当点P在BC上时, 求出P点坐标即可;(3)根据直角三角形的性质和点坐标列出解析式解出即可.
,当点P在OC上时,求出P点坐标,当点P在BC上时, 求出P点坐标即可;(3)根据直角三角形的性质和点坐标列出解析式解出即可.
![]() 点A的坐标为
点A的坐标为![]() ,
,
![]() 设直线AB的解析式为
设直线AB的解析式为![]() ,
,
![]() 点
点![]() 在直线AB上,
在直线AB上,
![]() ,
,
![]() ,
,
![]() 直线AB的解析式为
直线AB的解析式为![]() ;
;
![]() 由
由![]() 知,直线AB的解析式为
知,直线AB的解析式为![]() ,
,
令![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ,
,
![]() ,
,
设P的纵坐标为m,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线OC的解析式为
直线OC的解析式为![]() ,
,
当点P在OC上时,![]() ,
,
![]() ,
,
当点P在BC上时,![]() ,
,
![]() ,
,
即:点![]() 或
或![]() ;
;
![]() 是直角三角形,
是直角三角形,
![]() ,
,
当点P在OC上时,由![]() 知,直线OC的解析式为
知,直线OC的解析式为![]() ,
,
![]() 直线BP的解析式的比例系数为
直线BP的解析式的比例系数为![]() ,
,
![]() ,
,
![]() 直线BP的解析式为
直线BP的解析式为![]() ,
,
联立![]() ,解得
,解得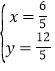 ,
,
![]() ,
,
当点P在BC上时,由![]() 知,直线AB的解析式为
知,直线AB的解析式为![]() ,
,
![]() 直线OP的解析式为
直线OP的解析式为![]() ,联立
,联立![]() 解得,
解得,![]() ,
,
![]() ,
,
即:点P的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市统计局发布的2016年《深圳市气候数据每日观测记录》显示,2016年12月26—21日这六天的平均相对湿度(百分数)分别是58,50,45,54,64,82.对于这组数据,以下说法正确的是( )
A.平均数是59
B.中位数是56
C.众数是82
D.方差是37 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①是一个重要公式的几何解释.请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B、C、D三点在一条直线上.试证明∠ACE=90°;
(3)伽菲尔德(G a rfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:
 =
= (a≠0),即a的负P次幂等于a的p次幂的倒数.例:
(a≠0),即a的负P次幂等于a的p次幂的倒数.例: =
=
(1)计算:
 =__;
=__; =__;
=__;(2)如果
 =
= ,那么p=__;如果
,那么p=__;如果 =
= ,那么a=__;
,那么a=__;(3)如果
 =
= ,且a、p为整数,求满足条件的a、p的取值.
,且a、p为整数,求满足条件的a、p的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】潜山市某村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )

A. 1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少
B. 1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平
C. 1月至3月每月生产总量逐月增加,4、5两月均停止生产
D. 1月至3月每月生产总量不变,4、5两月均停止生产
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是( )
A.
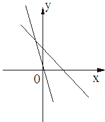 B.
B. 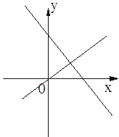
C.
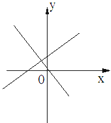 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列不等式化为“x>a”或“x<a”的形式:
(1)x+6>5; (2)3x>2x+2; (3)-2x+1<x+7; (4)-
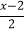 <
<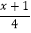 .
.
相关试题

