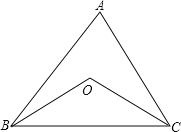
【题目】如图,在等腰△ABC中,∠A=80°,∠B和∠C的平分线相交于点O
(1)连接OA,求∠OAC的度数;
(2)求:∠BOC。
参考答案:
【答案】(1) 40°;(2) 130°
【解析】
试题(1)连接AO,利用等腰三角形的对称性即可求得∠OAC的度数;(2)利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系,再把∠A代入即可求∠BOC的度数.
试题解析:
(1)连接AO,
∵在等腰△ABC中,∠B和∠C的平分线相交于点O,
∴等腰△ABC关于线段AO所在的直线对称,
∵∠A=80°,
∴∠OAC=40°
(2)∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC= ∠ABC,∠OCB=∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-( ∠ABC+∠ACB)
=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=90°+∠A。
∴当∠A=80°时,
∠BOC=180° (∠B+∠C)=90°+∠A=130°。
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

-
科目: 来源: 题型:
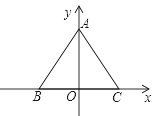
查看答案和解析>>【题目】如图,已知等边△ABC的边长为a,B,C在x轴上,A在y轴上.
(1)作△ABC关于x轴的对称图形△A′B′C′;
(2)求△ABC各顶点坐标和△A′B′C′各顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长为28cm,其中的一边长是另一边长的
 倍,求这个等腰三角形各边的长.
倍,求这个等腰三角形各边的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣(2m+1)+(
 m2﹣1).
m2﹣1).
(1)求证:不论m取什么实数,该二次函数图象与x轴总有两个交点;
(2)若该二次函数图象经过点(2m﹣2,﹣2m﹣1),求该二次函数的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,∠A=60°,BD⊥AC于点D,DG∥AB,DG交BC于点G,点E在BC的延长线上,且CE=CD.
(1)求∠ABD和∠BDE的度数;
(2)写出图中的等腰三角形(写出3个即可).

-
科目: 来源: 题型:
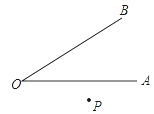
查看答案和解析>>【题目】如图,已知∠AOB=a外有一点P,画点P关于直线OA的对称点P′,再作点P′关于直线OB的对称点P″.
(1)试猜想∠POP″与a的大小关系,并说出你的理由.
(2)当P为∠AOB 内一点或∠AOB边上一点时,上述结论是否成立?
相关试题

