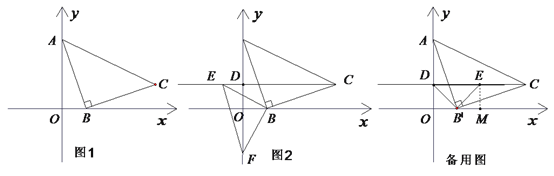
【题目】如图,在平面直角坐标系中,点 A,B的坐标分别为(0,3),(1,0),△ABC是等腰直角三角形,∠ABC=90°.
(1)图1中,点C的坐标为 ;
(2)如图2,点D的坐标为(0,1),点E在射线CD上,过点B 作BF⊥BE交y轴于点F.
①当点E为线段CD的中点时,求点F的坐标;
②当点E在第二象限时,请直接写出F点纵坐标y的取值范围.

参考答案:
【答案】(1 ) C(4,1);(2)①F( 0 , 1 ),②![]()
【解析】试题分析: ![]() 过点
过点![]() 向
向![]() 轴作垂线,通过三角形全等,即可求出点
轴作垂线,通过三角形全等,即可求出点![]() 坐标.
坐标.
![]() 过点E作EM⊥x轴于点M,根据
过点E作EM⊥x轴于点M,根据![]() 的坐标求出点
的坐标求出点![]() 的坐标,OM=2,得到
的坐标,OM=2,得到![]()
![]() 得到△OBF为等腰直角三角形,即可求出点
得到△OBF为等腰直角三角形,即可求出点![]() 的坐标.
的坐标.
![]() 直接写出
直接写出![]() 点纵坐标
点纵坐标![]() 的取值范围.
的取值范围.
试题解析:(1 ) C(4,1),
(2)法一:过点E作EM⊥x轴于点M,
∵C(4,1),D(0,1),E为CD中点,
∴CD∥x轴,EM=OD=1,
![]()
∴OM=2,
![]()
![]()
![]()
![]()
∴∠OBF=45°,
∴ △OBF为等腰直角三角形,
∴OF=OB=1.
![]()
法二:在OB的延长线上取一点M.
∵∠ABC=∠AOB=90°.
∴∠ABO+∠CBM=90° .
∠ABO+∠BAO =90°.
∴∠BAO=∠CBM .
∵C(4,1).
D(0,1).
又∵CD∥OM ,CD=4.
∴∠DCB=∠CBM.
∴∠BAO=∠ECB.
∵∠ABC=∠FBE=90°.
∴∠ABF=∠CBE.
∵AB=BC.
∴△ABF≌△CBE(ASA).
∴AF=CE=![]() CD=2,
CD=2,
∵A(0,3),
OA=3,
∴OF=1.
∴F(0,1) ,
(3) ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查方式,你认为最合适的是( )
A.日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.了解深圳市居民日平均用水量,采用全面调查方式
D.了解深圳市每天的平均用电量,采用抽样调查方式
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中是真命题的是( )
A.相等的角是对顶角B.两条直线被第三条直线所截,同位角相等
C.实数与数轴上的点是一一对应的D.垂直于同一条直线的两条直线互相平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习了“乘方”运算,下面介绍一种新运算,即“对数”运算.
定义:如果
 (a>0,a≠1,N>0),那么b叫做以a为底N的对数,记作
(a>0,a≠1,N>0),那么b叫做以a为底N的对数,记作 .
.例如:因为
 ,所以
,所以 ;因为
;因为 ,所以
,所以 .
.根据“对数”运算的定义,回答下列问题:
(1)填空:
 ,
,  .
.(2)如果
 ,求m的值.
,求m的值.(3)对于“对数”运算,小明同学认为有“
 (a>0,a≠1,M>0,N>0)”,他的说法正确吗?如果正确,请给出证明过程;如果不正确,请说明理由,并加以改正.
(a>0,a≠1,M>0,N>0)”,他的说法正确吗?如果正确,请给出证明过程;如果不正确,请说明理由,并加以改正. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点M(a + 5,a﹣3 )在y轴上,则点M的坐标为____,到x轴的距离为______.
-
科目: 来源: 题型:
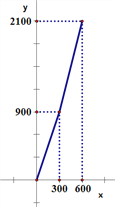
查看答案和解析>>【题目】随着人民生活水平的提高,越来越多的家庭采取分户式采暖,降低采暖用气价格的呼声强烈.某市物价局对市区居民管道天然气阶梯价格制度的规定作出了调整,调整后的付款金额y(单位:元)与年用气量(单位:m3)之间的函数关系如图所示:
(1)宸宸家年用气量是270m3,求付款金额.
(2)皓皓家去年的付款金额是1300元,求去年的用气量.
相关试题

