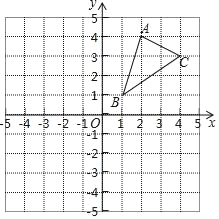
【题目】(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2.
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
参考答案:
【答案】(1)如图见解析,△A1B1C1为所作,点A1的坐标为(2,﹣4);(2)如图,△A2BC2为所作;见解析;(3)C点旋转到C2点所经过的路径长为![]() π.
π.
【解析】
(1)根据关于x轴对称的点的坐标特征求出A1、 B1、 C1的坐标, 进而画出图形;
(2)根据旋转作图的方法画出图形即可, 注意是逆时针旋转;
(3)根据 (2) 中的图形, 可知点C到C2的路径是一条弧线, 回想弧长的计算公式;
根据两点间的坐标公式求出BC的长, 再结合旋转的角度为90![]() , 利用弧长计算公式求解即可.
, 利用弧长计算公式求解即可.
(1)如图,△A1B1C1为所作,点A1的坐标为(2,﹣4);
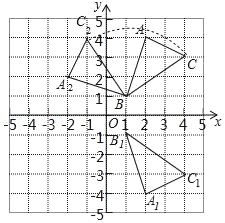
(2)如图,△A2BC2为所作;
(3)∵BC=![]() =
=![]() ,
,
∴C点旋转到C2点所经过的路径长为![]() =
=![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知小正方形
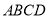 的面积为1,把它的各边延长一倍得新正方形
的面积为1,把它的各边延长一倍得新正方形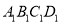 ;把正方形
;把正方形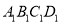 边长按原法延长一倍得到正方形
边长按原法延长一倍得到正方形 如图(2);以此下去,则正方形
如图(2);以此下去,则正方形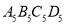 的面积为_________________.
的面积为_________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
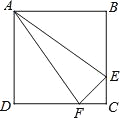
A.
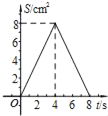 B.
B. 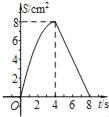
C.
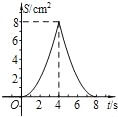 D.
D. 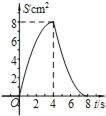
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②b<a﹣c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b),(m≠1的实数)⑥2a+b+c>0,其中正确的结论的有( )
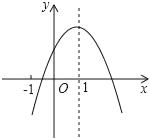
A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校想知道九年级学生对我国倡导的“一带一路”的了解程度,随机抽取部分九年级学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):A.非常了解.B.了解.C.知道一点.D.完全不知道.将调查的结果绘制如下两幅不完整的统计图,请根据两幅统计图中的信息,解答下列问题:
(1)求本次共调查了多少学生?
(2)补全条形统计图;
(3)该校九年级共有600名学生,请你估计“了解”的学生约有多少名?
(4)在“非常了解”的3人中,有2名女生,1名男生,老师想从这3人中任选两人做宣传员,请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为□ABCD的对角线,按要求完成下列各题.
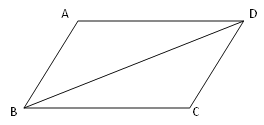
(1)用直尺和圆规作出对角线BD的垂直平分线交AD于点E,交BC于点F,垂足为O.(保留作图痕迹,不要求写作法)
(2)在(1)的基础上,连接BE和DF.求证:四边形BFDE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.

相关试题

