【题目】(一)知识链接
若点M,N在数轴上,且M,N代表的实数分别是a,b,则线段MN的长度可表示为 .
(二)解决问题
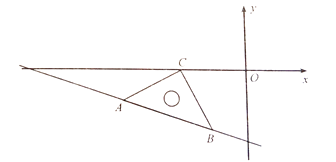
如图,将一个三角板放置在平面直角坐标系中,∠ACB=90°,AC=BC,点B,C的坐标分别为(-2,-4),(-4,0).
(1)求点A的坐标及直线AB的表达式;
(2)若P是x轴上一点,且S△ABP=6,求点P的坐标.
参考答案:
【答案】(一)![]() ;(二)(1)
;(二)(1)![]() ;
;![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(一)根据题意无法确定![]() 和
和![]() 的正负,因此线段MN的长度可表示为
的正负,因此线段MN的长度可表示为![]() ;
;
(二)(1)首先设点A的坐标为![]() ,根据已知条件列出二元一次方程组,解得即可;设直线AB的表达式为
,根据已知条件列出二元一次方程组,解得即可;设直线AB的表达式为![]() ,将A、B坐标代入即得解;
,将A、B坐标代入即得解;
(2)首先设点P的坐标为![]() ,
,![]() 的高为
的高为![]() ,根据
,根据![]() 的面积列出等式,即可解得.
的面积列出等式,即可解得.
解:(一)![]()
根据题意,无法确定![]() 和
和![]() 的正负,因此线段MN的长度可表示为
的正负,因此线段MN的长度可表示为![]() ;
;
(二)(1)设点A的坐标为![]()
∵∠ACB=90°,AC=BC,点B,C的坐标分别为(-2,-4),(-4,0)
∴![]()
∴![]()
∴![]() ,
,![]()
联立方程组,即为![]()
解得![]() 或
或![]() (A在第三象限,故舍去)
(A在第三象限,故舍去)
故点A坐标为![]() ;
;
设直线AB的表达式为![]() ,将A、B坐标代入即得
,将A、B坐标代入即得
![]()
解得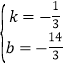
故AB的表达式为![]() .
.
(2)设点P的坐标为![]() ,
,![]() 的高为
的高为![]() ,
,
则![]() 即为点P到直线AB的距离,
即为点P到直线AB的距离,
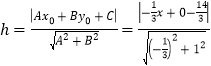 ①
①
又∵S△ABP=6,
∴![]()
∴![]() ②
②
联立①②,解得![]() 或
或![]()
故点P坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程mx2-2mx+m-2=0.
(1)若方程有两个不等实数根,求m的取值范围;
(2)若方程的两实数根为x1,x2,且|x1-x2|=1,求m的值.
-
科目: 来源: 题型:
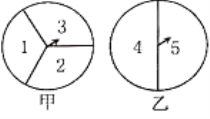
查看答案和解析>>【题目】如图,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏.规定小夏转甲盘一次、小秋转乙盘一次为一次游戏(当指针指在边界线上时视为无效,重转).
(1)小夏说:“如果两个指针所指区域内的数之和为6或7,则我获胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则,并用一种合适的方法(例如:树状图,列表)说明其公平性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为开展全科大阅读活动,学校花费了3400元在书店购买了40套古典文学书籍和20套现代文学书籍,每套现代文学书籍比每套古典文学书籍多花20元.
(1)求每套古典文学习书籍和现代文学书籍分别是多少元?
(2)为满足学生的阅读需求,学校计划用不超过2500元再次购买古典文学和现代文学书籍共40套,经市场调查得知,每套古典文学书籍价格上浮了20%,每套现代文学书籍价格下调了10%,学校最多能购买多少套现代文学书籍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为
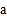 ,
,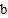 ,
,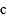 ,
,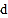 ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为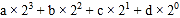 .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为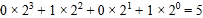 ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,平行四边形
 中,对角线
中,对角线 的垂直平分线分别交
的垂直平分线分别交 、
、 于点
于点 、
、 ,连接
,连接 、
、 ;
;

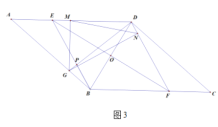
(1)如图1,求证:四边形
 是菱形;
是菱形;(2)如图2,当
 ,点
,点 在
在 上,连接
上,连接 ,使
,使 ,过点
,过点 作
作 于点
于点 ,作
,作 于点
于点 ,连接
,连接 ,求证:
,求证: ;
;(3)如图3,在(2)的条件下,
 交
交 于点
于点 ,若
,若 ,
, ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,在边长为1的正方形
 的边上有—动点
的边上有—动点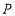 沿正方形运动一周,
沿正方形运动一周,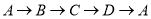 则
则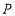 的纵坐标
的纵坐标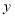 与点
与点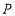 走过的路程
走过的路程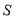 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )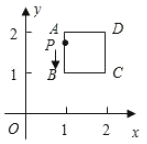
A.
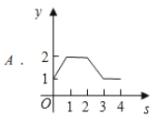 B.
B. 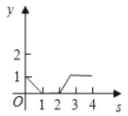 C.
C. 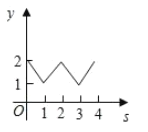 D.
D. 
相关试题

