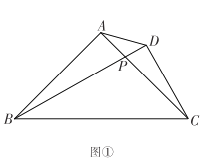
【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .

参考答案:
【答案】![]() 或
或![]()
【解析】
当△![]() 为直角三角形时,存在两种情况:
为直角三角形时,存在两种情况:
①当![]() 时,如图1,根据对称的性质和平行线可得:
时,如图1,根据对称的性质和平行线可得:![]() ,根据直角三角形斜边中线的性质得:
,根据直角三角形斜边中线的性质得:![]() ,最后利用勾股定理可得
,最后利用勾股定理可得![]() 的长;
的长;
②当![]() 时,如图2,证明
时,如图2,证明![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() .
.
解:当△![]() 为直角三角形时,存在两种情况:
为直角三角形时,存在两种情况:
①当![]() 时,如图1,
时,如图1,
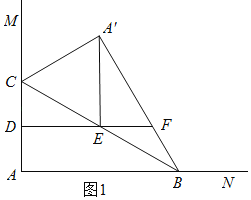
![]() △
△![]() 与
与![]() 关于
关于![]() 所在直线对称,
所在直线对称,
![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
![]() 、
、![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() △
△![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,
的中点,
![]() ,
,
由勾股定理得:![]() ,
,
![]() ;
;
②当![]() 时,如图2,
时,如图2,
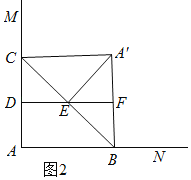
![]() ,
,
![]() ,
,
![]() △
△![]() 与
与![]() 关于
关于![]() 所在直线对称,
所在直线对称,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ;
;
综上所述,![]() 的长为
的长为![]() 或4;
或4;
故答案为:![]() 或4;
或4;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在反比例函数y=
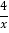 (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y=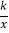 (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )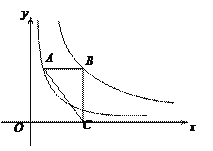
A. 10 B. 12 C. 14 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形
 中,
中, 、
、 分别是边
分别是边 、
、 的中点,
的中点, 分别交
分别交 、
、 于
于 、
、 .请判断下列结论:
.请判断下列结论: ;
; ;
; ;
; .其中正确的结论有( )
.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初三学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.

 求这次调查的家长人数,并补全条形图;
求这次调查的家长人数,并补全条形图; 求扇形图中表示家长“赞成”的圆心角的度数;
求扇形图中表示家长“赞成”的圆心角的度数; 若某地区共有初三学生
若某地区共有初三学生 名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数约是多少?
名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数约是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和爸爸周末步行去游泳馆游泳,爸爸先出发了一段时间后小明才出发,途中小明在离家
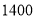 米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.爸爸、小明离家的距离
米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.爸爸、小明离家的距离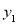 (单位:米),
(单位:米),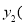 单位:米)与小明所走时间
单位:米)与小明所走时间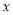 (单位:分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:
(单位:分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:
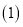 分别求出爸爸离家的距离
分别求出爸爸离家的距离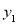 和小明到达报亭前离家的距离
和小明到达报亭前离家的距离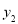 与时间
与时间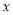 之间的函数关系式;
之间的函数关系式;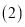 求小明在报亭休息了多长时间遇到姗姗来迟的爸爸?
求小明在报亭休息了多长时间遇到姗姗来迟的爸爸? 若游泳馆离小明家
若游泳馆离小明家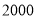 米,请你通过计算说明谁先到达游泳馆?
米,请你通过计算说明谁先到达游泳馆? -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中,  是直线
是直线 上的一点,连接
上的一点,连接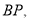 过点
过点 作
作 交直线
交直线 于点
于点 .
. 当点
当点 在线段
在线段 上时,如图①,求证:
上时,如图①,求证: ;
;
 当点
当点 在直线
在直线 上移动时,位置如图②、图③所示,线段
上移动时,位置如图②、图③所示,线段 与
与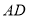 之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
相关试题

