【题目】在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
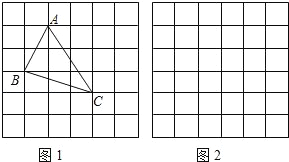
(1)请你将△ABC的面积直接填写在横线上
(2)画△DEF,DE、EF、DF三边的长分别为![]() 、
、![]() 、
、![]()
①判断三角形的形状,说明理由.
②求这个三角形的面积.
参考答案:
【答案】(1)3.5;(2)△DEF为直角三角形;理由见解析;2.
【解析】
试题分析:(1)利用恰好能覆盖△ABC的边长为3的小正方形的面积减去三个小直角三角形的面积即可解答;
(2)①利用勾股定理的逆定理进行解答,②利用(1)方法解答就可以解决问题.
试题解析:(1)如图,
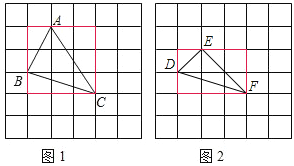
S△ABC=3×3-![]() ×3×1-
×3×1-![]() ×2×1-
×2×1-![]() ×3×2=3.5;
×3×2=3.5;
(2)①△DEF为直角三角形;
因为(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2,
)2,
所以△DEF为直角三角形;
②S△DEF=3×2-![]() ×3×1-
×3×1-![]() ×2×2-
×2×2-![]() ×1×1=2;
×1×1=2;
答:△DEF的面积为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=(
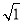 )2+1=2 S1=
)2+1=2 S1=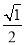 ;
;OA32=(
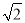 )2+1=3 S2=
)2+1=3 S2=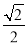 ;
;OA42=(
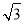 )2+1=4 S3=
)2+1=4 S3=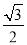 …
…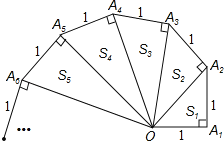
(1)请用含有n(n为正整数)的等式Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF,相似比为3:5,△ABC的周长为6,则△DEF的周长为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a3mb和 - 2a6bn+2是同类项,化简并求值:2(m2 - mn) - 3(2m2 - 3mn) - 2[m2 - (2m2 - mn+m2)] - 1.
-
科目: 来源: 题型:
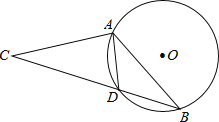
查看答案和解析>>【题目】如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
A.2﹣
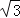 B.
B.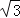 ﹣1 C.2 D.
﹣1 C.2 D.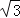 +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型
B型
价格(万元/台)
12
10
月污水处理能力(吨/月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的价格标签已丢失,售货员只知道“它的进价为80元,打七折售出后,仍可获利4元”,你认为售货员应标在标签上的价格是______________.
相关试题

